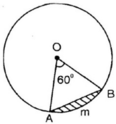
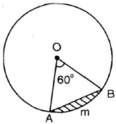
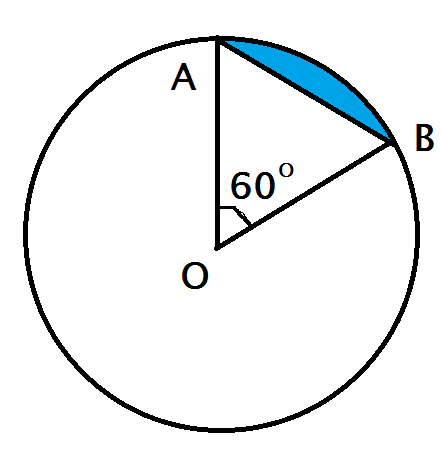
Gỉa sử mặt đồng hồ là một hình tròn tâm O, bán kính R, kim giờ và kim phút và 2 bán kính OA và OB. Diện tích hình viên phân giới hạn bởi dây AB và cung nhỏ AB khi đồng hồ chỉ 9 giờ đúng là .... R2 (đvdt)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 6 2018
Tam giác OAB là tam giác đều có cạnh R= 5,1 cm.
Công thức tính diện tích tam giác đều cạnh a là: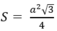 
Do đó, diện tích tam giác đều OAB cạnh OA= R = 5,1 cm là: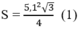 
Diện tích hình quạt tròn AOB là:
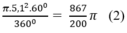
Từ (1) và (2) suy ra diện tích hình viên phân là:
CM
20 tháng 8 2019
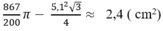
Tam giác OAB là tam giác đều có cạnh R= 5,1 cm.
Công thức tính diện tích tam giác đều cạnh a là: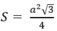 
Do đó, diện tích tam giác đều OAB cạnh OA= R = 5,1 cm là: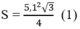 
Diện tích hình quạt tròn AOB là:
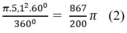
Từ (1) và (2) suy ra diện tích hình viên phân là:
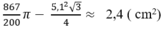
Kiến thức áp dụng
+ Diện tích tam giác đều cạnh a là:
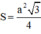
+ Diện tích hình quạt tròn bán kính R, cung nº được tính theo công thức:
HN
27 tháng 3 2022
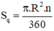
\(\widehat{BAC}=60^o\Rightarrow\widehat{BOC}=120^o\). Diện tích cần tìm là \(\pi\).32-1/2.3.3.sin120o=9\(\pi\)-9\(\sqrt{3}\)/4 (cm2)\(\approx\)24,38 (cm2).
13 tháng 4 2017
Hướng dẫn giải:
∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diện tích tam giác đều cạnh a là a2√44 ta có
S∆OBC = SΔOBC=R2√34 (1)
Diện tích hình quạt tròn AOB là:
π.R2.6003600=πR26 (2)
Từ (1) và (2) suy ra diện tích hình viên phân là:
πR26−R2√34=R2(π6−√34)
Thay R = 5,1 ta có Sviên phân ≈ 2,4 (cm2)
2 tháng 7 2023
góc AOB=180-60=120 độ
S OAB=1/2*OA*OB*sinAOB=\(R^2\cdot\dfrac{\sqrt{3}}{4}\)
S q OAB=\(pi\cdot R^2\cdot\dfrac{120}{360}=pi\cdot R^2\cdot\dfrac{1}{3}\)
=>\(Svp=R^2\left(pi\cdot\dfrac{1}{3}-\dfrac{\sqrt{3}}{4}\right)\)
23 tháng 12 2021
Câu 1:
- Khái niệm bài toán: là 1 công việc hay 1 nhiệm vụ cần được giải quyết. - Xác định bài toán là đi xác định điều kiện cho trước và xác định kết quả cần thu được.