3. Tia sáng truyền từ một chất rong suốt có chiết suất n tới mặt phân cách với môi trường ko khí. Góc khúc xạ trong ko khí là 60. Tia phản xạ ở mặt phân cách có phương vuông góc với tia khúc xạ . Chiết suất n là.
5. Một thấu kính có độ tụ D= 2 dp , biết vật thật đặt vuông góc với trục chính của thấu kính và cách thấu kính 25cm . Ảnh qua thấu kính vị trí ảnh và độ phóng đại của ảnh là
A. ảnh thật , cách thấu kính 25cm , k=-1
B. Ảnh ảo , cách thấu kính 25cm , k=1
C. ảnh thật , cách thấu kính 50cm, k=-2
D. ảnh ảo , cách thấu kính 50cm, k=2
7. Thấu kính hội tụ có tiêu cự f . Khoảng cách ngắn nhất giữa vật thật và ảnh thật qua thấu kính là
A. 6f
B. 3f
C. 5f
D. 4f
8. Một thấu kính phân kì có tiêu cự bằng -20m . Độ tụ của thấu kính là
A. 5dp
B. 0,05 dp
C. -0,05dp
D. -5 dp.
15. Một vật sáng đặt trước 1 thấu kính , trên trục chính của thấu kính. Cho biết ảnh của vật tạo bởi thấu kính bằng 3 lần vật. Dịch chuyển vật lại gần thấu kính 1 đoạn 12cm thì thấy ảnh của vật ở vị trí mới vẫn bằng 3 lần vật . Tiêu cự của thấu kính là.
19. Chiếu 1 tia sáng đi tù ko kí vào 1 môi trường co chiết suất n , sao cho tia khcs xạ vuông góc vs tia phản xạ . Góc tới i trong trường hợp này đc xác định bởi công thức
A. tani=n
B. sini=1/n
C. tani=1/n
D. sini=n
22. Một thấu kính hội tụ có tiêu cự f=20cm. Vật sáng AB đc đặt trước thấu kính và có ảnh ảo A'B' . Biết khoảng cachs giữa vật và ảnh là 45cm. Vật cách thấu kính 1 đoạn là.


![LỜI GIẢI] Chiếu một tia sáng đơn sắc đi từ không khí vào môi trường có chiết suất n và góc tới i sao cho tia p - Tự Học 365](https://tuhoc365.vn/wp-content/uploads/2020/03/1-316.png)
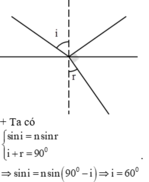
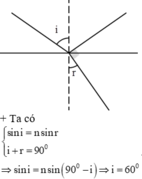
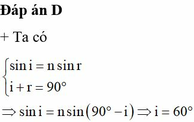
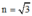

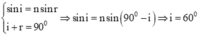


3/ \(n\sin i=\sin60^0;\) \(i=90-r\Rightarrow i=30^0\)
\(\Rightarrow n=\dfrac{\sin60^0}{\sin30^0}=\sqrt{3}\)
5/ \(D=\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow2=\dfrac{1}{0,25}+\dfrac{1}{d'}\Rightarrow d'=-50\left(cm\right)\)
\(k=-\dfrac{d'}{d}=\dfrac{50}{25}=2\)
=>D. Anh ao, cach thau kinh 50cm, k=2
7/ \(d=\dfrac{d'f}{d'-f}\Rightarrow d+d'=d'+\dfrac{d'f}{d'-f}=\dfrac{d'^2-d'f+d'f}{d'-f}=\dfrac{d'^2}{d'-f}\)
\(\left(d+d'\right)_{min}\Leftrightarrow(\dfrac{1}{d'}-\dfrac{f}{d'^2})_{max}\)
Dat \(\dfrac{1}{d'}=a\Rightarrow a-a^2f=-\left(a^2f+a+\dfrac{1}{4f}\right)+\dfrac{1}{4f}=-\left(a\sqrt{f}+\dfrac{1}{2\sqrt{f}}\right)^2\le\dfrac{1}{4f}\)
\("="\Leftrightarrow a\sqrt{f}=\dfrac{1}{2\sqrt{f}}\Leftrightarrow2af=1\Rightarrow a=\dfrac{1}{2f}\)
\(\Rightarrow\dfrac{1}{d'}=\dfrac{1}{2f}\Rightarrow d'=2f\Rightarrow d=\dfrac{d'f}{d'-f}=\dfrac{2f^2}{2f-f}=2f\)
\(\Rightarrow\left(d+d'\right)_{min}=2f+2f=4f\Rightarrow D.4f\)
8/ \(D=\dfrac{1}{f}=-\dfrac{1}{20}=-0,05\left(dp\right)\Rightarrow C.-0,05dp\)
15/ \(k_1=\dfrac{f}{f-d_1};k_2=\dfrac{f}{f-d_2};\dfrac{k_1}{k_2}=-1\)
\(d_2=d_1-12\Rightarrow\dfrac{k_1}{k_2}=-1=\dfrac{f-d_2}{f-d_1}=\dfrac{f-d_1-12}{f-d_1}\) (1)
\(\dfrac{1}{f}=\dfrac{1}{d_1}+\dfrac{1}{d_1'};-\dfrac{d'_1}{d_1}=3\Rightarrow\dfrac{1}{f}=\dfrac{1}{d_1}-\dfrac{1}{3d_1}\)
\(\Rightarrow\dfrac{1}{f}=\dfrac{2}{3d_1}\Rightarrow d_1=\dfrac{2}{3}f\)
Thay vo (1)\(\Rightarrow\dfrac{f-\dfrac{2}{3}f-12}{f-\dfrac{2}{3}f}=-1\Leftrightarrow\dfrac{1}{3}f-12=-\dfrac{1}{3}f\Rightarrow f=18\left(cm\right)\)
19/ \(\sin i=n\sin r=n\cos i\Rightarrow\tan i=n\Rightarrow A.\tan i=n\)
22/ \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow\dfrac{1}{20}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(-d'-d=45\Rightarrow d'=-d-45\Rightarrow\dfrac{1}{20}=\dfrac{1}{d}-\dfrac{1}{d+45}\)
\(\Leftrightarrow d^2+45d=45.20\Leftrightarrow\left[{}\begin{matrix}d=15\left(cm\right)\\d=-60\left(loai\right)\end{matrix}\right.\Rightarrow d'=-60\left(cm\right)\)