1+1+1x2+2x2=????????????????????????????
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 9 x 4 − 10 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 9 t 2 − 10 t + 1 = 0 ( 2 )
Giải (2):
Có a = 9 ; b = -10 ; c = 1
⇒ a + b + c = 0
⇒ Phương trình (2) có nghiệm t 1 = 1 ; t 2 = c / a = 1 / 9
Cả hai nghiệm đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1.
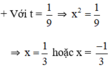
Vậy phương trình (1) có tập nghiệm 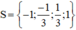
b)
5 x 4 + 2 x 2 - 16 = 10 - x 2 ⇔ 5 x 4 + 2 x 2 - 16 - 10 + x 2 = 0 ⇔ 5 x 4 + 3 x 2 - 26 = 0
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 5 t 2 + 3 t − 26 = 0 ( 2 )
Giải (2) :
Có a = 5 ; b = 3 ; c = -26
⇒ Δ = 3 2 − 4.5 ⋅ ( − 26 ) = 529 > 0
⇒ Phương trình có hai nghiệm phân biệt
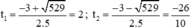
Đối chiếu điều kiện chỉ có t 1 = 2 thỏa mãn
+ Với t = 2 ⇒ ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2.
Vậy phương trình (1) có tập nghiệm S = {-√2; √2}
c) 0 , 3 x 4 + 1 , 8 x 2 + 1 , 5 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó, (1) trở thành : 0 , 3 t 2 + 1 , 8 t + 1 , 5 = 0 ( 2 )
Giải (2) :
có a = 0,3 ; b = 1,8 ; c = 1,5
⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm t 1 = − 1 và t 2 = − c / a = − 5
Cả hai nghiệm đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
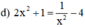
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được :
2 x 4 + x 2 = 1 − 4 x 2 ⇔ 2 x 4 + x 2 + 4 x 2 − 1 = 0 ⇔ 2 x 4 + 5 x 2 − 1 = 0 ( 1 )
Đặt t = x 2 , điều kiện t > 0.
Khi đó (1) trở thành : 2 t 2 + 5 t - 1 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 5 ; c = -1
⇒ Δ = 5 2 − 4.2 ⋅ ( − 1 ) = 33 > 0
⇒ Phương trình có hai nghiệm phân biệt:
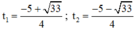
Đối chiếu với điều kiện thấy có nghiệm t 1 thỏa mãn.
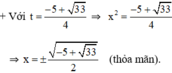
Vậy phương trình có tập nghiệm 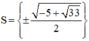

Ohhh, tui hiểu r.
x2 - x + \(\dfrac{1}{4}\)
⇔ x2 - 2.\(\dfrac{1}{2}\).x + \(\left(\dfrac{1}{2}\right)^2\)
⇔ \(\left(x^2-\dfrac{1}{2}\right)^2\)

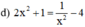
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được :
2x4 + x2 = 1 – 4x2
⇔ 2x4 + x2 + 4x2 – 1 = 0
⇔ 2x4 + 5x2 – 1 = 0 (1)
Đặt t = x2, điều kiện t > 0.
Khi đó (1) trở thành : 2t2 + 5t – 1 = 0 (2)
Giải (2) :
Có a = 2 ; b = 5 ; c = -1
⇒ Δ = 52 – 4.2.(-1) = 33 > 0
⇒ Phương trình có hai nghiệm phân biệt:
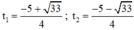
Đối chiếu với điều kiện thấy có nghiệm t1 thỏa mãn.
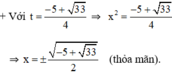
Vậy phương trình có tập nghiệm 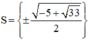

a) 2 x 2 − 2 x 2 + 3 x 2 − 2 x + 1 = 0 ( 1 )
Đặt x 2 – 2 x = t ,
(1) trở thành : 2 t 2 + 3 t + 1 = 0 ( 2 ) .
Giải (2) :
Có a = 2 ; b = 3 ; c = 1
⇒ a – b + c = 0
⇒ (2) có nghiệm t 1 = - 1 ; t 2 = - c / a = - 1 / 2 .
+ Với t = -1 ⇒ x 2 − 2 x = − 1 ⇔ x 2 − 2 x + 1 = 0 ⇔ ( x − 1 ) 2 = 0 ⇔ x = 1
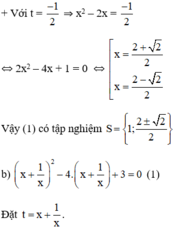
(1) trở thành: t 2 – 4 t + 3 = 0 ( 2 )
Giải (2):
Có a = 1; b = -4; c = 3
⇒ a + b + c = 0
⇒ (2) có nghiệm t 1 = 1 ; t 2 = c / a = 3 .
+ t = 1 ⇒ x + 1/x = 1 ⇔ x 2 + 1 = x ⇔ x 2 – x + 1 = 0
Có a = 1; b = -1; c = 1 ⇒ Δ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
Phương trình vô nghiệm.



Ta có: Δ = 4 m − 1 2 − 4.2. 2 m − 1 = 4 m − 3 2
2 x 2 + 2 x 2 − 4 m − 1 x 2 + 2 x + 2 m − 1 = 0
⇔ x 2 + 2 x = 1 2 ( 1 ) x 2 + 2 x = 2 m − 1 ( 2 )
( 1 ) ⇔ x 2 + 2 x − 1 2 = 0 ⇔ x = − 2 + 6 2 ∉ − 3 ; 0 x = − 2 − 6 2 ∈ − 3 ; 0
Do đó (1) chỉ có 1 nghiệm thuộc − 3 ; 0
Để phương trình đã cho có 3 nghiệm thuộc đoạn − 3 ; 0 thì phương trình (2) phải có hai nghiệm phân biệt thuộc đoạn và hai nghiệm này phải khác − 2 − 6 2
2 ⇔ x + 1 2 = 2 m
Phương trình (2) có hai nghiệm phân biệt khác − 2 − 6 2 và thuộc đoạn − 3 ; 0
⇔ 2 m > 0 − 2 − 6 2 + 1 2 ≠ 2 m − 3 ≤ − 1 + 2 m ≤ 0 − 3 ≤ − 1 − 2 m ≤ 0 ⇔ m > 0 m ≠ 3 4 m ≤ 1 2 m ≤ 2
Không có giá trị nào của m thỏa mãn.
Đáp án cần chọn là: D

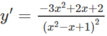
1+1+1x2+2x2 = 1+1+2+4 = 8 nhé ^^
nhé
1+1+2+4=8