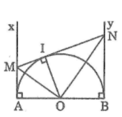
Cho nửa đường tròn tâm O,đường kính AB.Gọi Ax,By là các tia vuông góc với AB.Qua điểm E thuộc nửa đường tròn kẻ tiếp tuyến với nửa đường tròn cắt Ax và By lần lượt tại C và D
a)Chứng minh CD=AC+BD
b)Gọi I là giao điểm của OC và AE,gọi K là giao điểm của OD và BE.Tứ giác EIOK là hình gì?Vì sao?

a: Xet (O) có
CE,CA là các tiếp tuyến
nên CE=CA và OC là phân giác của góc EOA(1)
mà OE=OA
nên OC là trung trực của AE
=>OC vuông góc với AE
Xét (O) có
DE,DB là các tiếp tuyến
nen DE=DB và OD là phân giác của góc EOB(2)
mà OE=OB
nên OD là trung trực của BE
=>OD vuông góc với BE
CE+ED=CD
=>CD=CA+BD
b: Từ (1), (2) suy ra góc COD=1/2*180=90 độ
Xét tứ giác EIOK co
góc EIO=góc EKO=góc IOK=90 độ
nên EIOK là hình chữ nhật