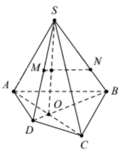
Cho hình chóp SABCD có đáy ABCD là tứ giác lồi. Gọi M, N là trung điểm SB, SD. Trên dường chéo AC ta lấy điểm K tùy ý. Tìm thiết diện của hình chóp cắt bởi (KMN).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


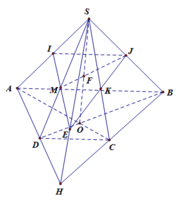
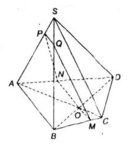
Trong (SAD) do \(\dfrac{SM}{SA}\ne\dfrac{SP}{SD}\left(\dfrac{1}{2}\ne\dfrac{3}{4}\right)\) nên MP không song song với AD
⇒ Giả sửa MP cắt AD tai E
⇒ E ∈ (ABCD)
Trong (ABCD) gọi K là giao điểm của EN và BC
Trong (ABCD) gọi O là giao điểm của AC và BD
⇒ SO ⊂ (SBD)
Gọi giao điểm của NK và AC là I
Trong (SAC) IM cắt SO tại H
Trong (SBD) DH cắt SB tại Q
⇒ Bla bla bla gì đó
⇒ Thiết diện cần tìm là ngũ giác MPNKQ

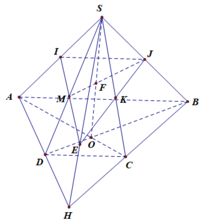
Trong tam giác SBD, MN là đường trung bình \(\Rightarrow MN||BD\)
\(\Rightarrow MN||\left(ABCD\right)\)
Trong mp (ABCD), qua E kẻ đường thẳng song song BD cắt BC tại F và cắt AD kéo dài tại G
Trong mp (SAD), nối GN kéo dài cắt SA tại P
Ngũ giác PNEFM là thiết diện của (MNE) và chóp

Lời giải:
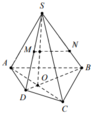
Gọi $Q$ là điểm nằm trên $DC$ sao cho $AD\parallel PQ$
Khi đó: $MN\parallel AD\parallel PQ$ nên $Q\in (MNP)$
$(MNPQ)$ chính là thiết diện của hình chóp cắt bởi $(MNP)$
Giờ ta cần tìm diện tích hình thang $MNPQ$
$SA=SD; DB=SC; AB=CD$ nên $\triangle SAB=\triangle SDC$
Tương ứng ta có $MP=NQ$
$MN=\frac{AD}{2}=\frac{3a}{2}$
$PQ=AD=3a$
$\Rightarrow MNPQ$ là hình thang cân.
Áp dụng định lý cos:
$\cos \widehat{SAB}=\frac{SA^2+AB^2-SB^2}{2SA.AB}=\frac{MA^2+AP^2-MP^2}{2MA.AP}$
$\Leftrightarrow \frac{9a^2+9a^2-27a^2}{2.3a.3a}=\frac{\frac{9}{4}a^2+4a^2-MP^2}{2.\frac{3}{2}a.2a}$
$\Rightarrow MP^2=\frac{37}{4}a^2$
$\Rightarrow h_{MNPQ}=\sqrt{MP^2-(\frac{PQ-MN}{2})^2}=\frac{\sqrt{139}}{4}a$
Diện tích thiết diện:
$S=\frac{MN+PQ}{2}.h=\frac{9\sqrt{139}}{16}a^2$

Đáp án D
Dựa vào hình vẽ, ta thấy 2 đường thẳng MN và SO cắt nhau. Các cặp đường thẳng (SO;AD),(MN;SC),(SA;BC) chéo nhau

+ Ta có: (α) // AB
⇒ giao tuyến (α) và (ABCD) là đường thẳng qua O và song song với AB.
Qua O kẻ MN // AB (M ∈ BC, N ∈ AD)
⇒ (α) ∩ (ABCD) = MN.
+ (α) // SC
⇒ giao tuyến của (α) và (SBC) là đường thẳng qua M và song song với SC.
Kẻ MQ // SC (Q ∈ SB).
+ (α) // AB
⇒ giao tuyến của (α) và (SAB) là đường thẳng qua Q và song song với AB.
Từ Q kẻ QP // AB (P ∈ SA).
⇒ (α) ∩ (SAD) = PN.
Vậy thiết diện của hình chóp cắt bởi (α) là tứ giác MNPQ.
Ta có: PQ// AB và NM // AB
=> PQ // NM
Do đó, tứ giác MNPQ là hình thang.