Mọi người ơi giúp mik với ạ . Cho mik đáp án đúng nhất với ạ, xng thì mik sẽ tick ,mik cảm ơn ạ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC có BM/BC=BD/BA
nên MD//AC
=>MM' vuông góc AB
=>M đối xứngM' qua AB
b: Xét tứ giác AMBM' có
D là trung điểm chung của AB và MM'
MA=MB
Do đó: AMBM' là hình thoi

a: ĐKXĐ: x<>2; x<>-3
b: \(P+\dfrac{x^2-4-5-x-3}{\left(x-2\right)\left(x+3\right)}=\dfrac{\left(x-4\right)\left(x+3\right)}{\left(x-2\right)\left(x+3\right)}=\dfrac{x-4}{x-2}\)
c: Để P=-3/4 thì x-4/x-2=-3/4
=>4x-8=-3x+6
=>7x=14
=>x=2(loại)
e: x^2-9=0
=>x=3 (nhận) hoặc x=-3(loại)
Khi x=3 thì \(P=\dfrac{3-4}{3-2}=-1\)

a: \(Q=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-2\sqrt{x}\left(\sqrt{x}-2\right)-5\sqrt{x}-2}{x-4}:\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)}{\left(\sqrt{x}+2\right)^2}\)
\(=\dfrac{x+3\sqrt{x}+2-2x+4\sqrt{x}-5\sqrt{x}-2}{x-4}\cdot\dfrac{\left(\sqrt{x}+2\right)^2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(=\dfrac{-x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}\left(3-\sqrt{x}\right)}\)
\(=\dfrac{-\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\cdot\left(-1\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}-3}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
b: Khi x=4-2căn 3 thì \(Q=\dfrac{\sqrt{3}-1+2}{\sqrt{3}-1-3}=\dfrac{\sqrt{3}+1}{\sqrt{3}-4}=\dfrac{-7-5\sqrt{3}}{13}\)
c: Q>1/6
=>Q-1/6>0
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}-3}-\dfrac{1}{6}>0\)
=>\(\dfrac{6\sqrt{x}+12-\sqrt{x}+3}{6\left(\sqrt{x}-3\right)}>0\)
=>\(\dfrac{5\sqrt{x}+9}{6\left(\sqrt{x}-3\right)}>0\)
=>căn x-3>0
=>x>9

a: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)
b: \(=\dfrac{x^2-2x-3+x^2+2x-3+2x-2x^2}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{2x-6}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x+3}\)
c: \(=\dfrac{6-7+x}{3\left(x-1\right)}=\dfrac{x-1}{3\left(x-1\right)}=\dfrac{1}{3}\)
d: \(=\dfrac{x^3+2x+2x-2-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^3-x^2+3x-3}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{x^2+3}{x^2+x+1}\)

\(\dfrac{1}{x^2-4}+\dfrac{2x}{x+2}=\dfrac{1}{\left(x-2\right)\left(x+2\right)}+\dfrac{2x}{x+2}=\dfrac{1+2x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{1+2x^2-4x}{\left(x+2\right)\left(x-2\right)}\)
trên bài mink đã ẩn đi bước quy đồng!!
\(\dfrac{18}{\left(x-3\right)\left(x^2-9\right)}-\dfrac{3}{x^2-6x+9}-\dfrac{x}{x^2-9}=\dfrac{18}{\left(x-3\right)\left(x+3\right)\left(x-3\right)}-\dfrac{3}{\left(x-3\right)^2}-\dfrac{x}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{18}{\left(x-3\right)^2\left(x+3\right)}-\dfrac{3}{\left(x-3\right)^2}-\dfrac{x}{\left(x-3\right)\left(x+3\right)}=\dfrac{18-3\left(x+3\right)-x\left(x-3\right)}{\left(x-3\right)^2\left(x+3\right)}\)
\(=\dfrac{18-3x-9-x^2+3x}{\left(x-3\right)^2\left(x+3\right)}=\dfrac{9-x^2}{\left(x-3\right)^2\left(x+3\right)}=\dfrac{-\left(x-3\right)\left(x+3\right)}{\left(x-3\right)^2\left(x+3\right)}=\dfrac{-1}{x-3}\)

a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: \(HD=\sqrt{10^2-8^2}=6\left(cm\right)\)
\(S_{ADHE}=6\cdot8=48\left(cm^2\right)\)
c: Để ADHE là hình vuông thì AH là phân giác của góc BAC
=>góc B=45 độ





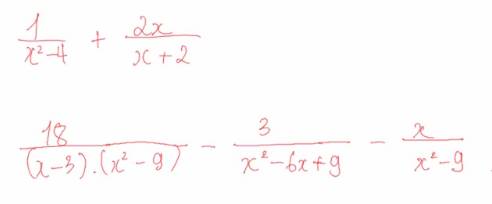



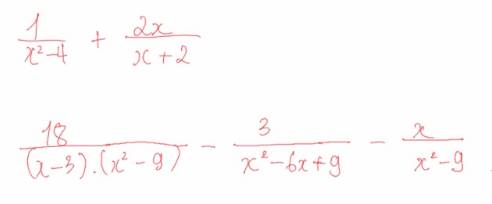
2 A
3 D
4 A
5 A
6 B
7 A
8 A
9 A