Cho hình tam giác ABC có diện tích 36 cm2 . Điểm M và N lần lượt là trung điểm của BC và AC. Tính diện tích hình tam giác CMN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 2 2017
nối A với M. diện tích tam giác ACM bằng 1/2 ABC vì chung chiều cao hạ từ đỉnh A xuống đáy CB và CM là trung điểm của CB.
diện tích tam giác NCM bằng một nửa diện tích tam giác ACM vì chung chiều cao hạ từ đỉnh M xuống đáy AC và AN là trung điểm của AC.
diện tích ACM :......
diện tích NCM :.......
đáp số
AH
Akai Haruma
Giáo viên
5 tháng 2
Lời giải:
Ta có:
$\frac{S_{CMN}}{S_{CAM}}=\frac{NC}{AC}=\frac{1}{2}$
$\frac{S_{CAM}}{S_{ABC}}=\frac{CM}{BC}=\frac{1}{2}$
$\Rightarrow \frac{S_{CMN}}{S_{CAM}}\times \frac{S_{CAM}}{S_{ABC}}=\frac{1}{2}\times \frac{1}{2}$
$\Rightarrow \frac{S_{CMN}}{S_{ABC}}=\frac{1}{4}$
$S_{CMN}=\frac{1}{4}\times S_{ABC}=150:4=37,5$ (cm2)
6 tháng 3 2019
Diện tích tam giác ABN = 1/4 diện tích tam giác ABC vì có chung chiều cao nối từ A xuống N và BN = 1/4 BC
Diện tích tam giác ABN là:
64 x 1/4 = 16 (cm2 )
Diện tích tam giác BMN = 1/2 diện tích tam giác ABN vì có chung chiều cao nối từ N xuống M và BM = 1/2 BA
Diện tích tam giác BMN là:
16 x 1/2 = 8 (cm2 )
Đáp số: 8 cm2
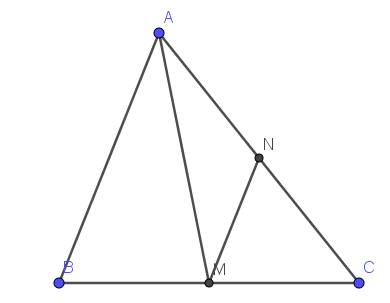
S(CMN) = S(AMN) có AN = NC và chung đường cao tương ứng với đáy AC
S(CMN) = 1/2 S(AMC)
S(AMC) = S(ABM) có CM = MB và chung đường cao tương ứng với đáy BC
S(AMC) = 1/2 S(ABC)
Nên S(CMN) = 1/S(ABC)
DT tam giác CMN :
36 : 4 = 9 cm2