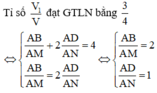A vẽ hình chóp S,ABCD đáy ABCD là hình bình hàng B :vẽ hình chóp cụt ABCD .ABCD đáy lớn ABCD là hình bình hành
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


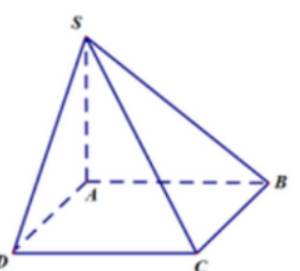
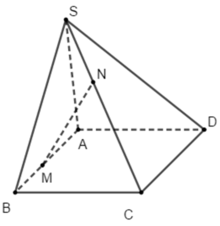
Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn của nó cũng có các mặt bên là hình tam giác.
ABCD là hình bình hành nên hình biểu diễn của nó cũng là hình bình hành
Từ đó, ta vẽ được hình biểu diễn của hình chóp S.ABCD

1: Số mặt bên là 4
\(SAB;SAD;SBC;SCD\)
2: Số cạnh đáy là 4
AB,BC,CD,DA
3: SA và BC là hai đường thẳng chéo nhau
4: 4 đỉnh: A,B,C,D
5: Có 7 mặt: \(SAB;SAD;SBC;SCD;SAC;SBD;ABCD\)
6C

![]()
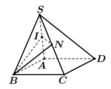
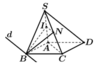
Ta có IN là đường trung bình của ∆ S A C nên IN//AC
Lại có ![]()
Do đó: IN//AC//d
Vậy giao tuyến của hai mặt phẳng (BIN) và (ABCD) là đường thẳng d đi qua B và song song với AC
Chọn A.

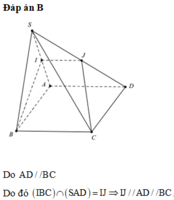
Đáp án B
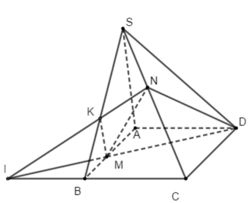
Trong mặt phẳng (ABCD) gọi I là giao điểm của MD và BC
Trong mặt phẳng (SBC) gọi K là giao điểm của IN và SB
Khi đó ta có: (MND) ∩ (SAB) = KM
(MND) ∩ (ABCD) = MD
(MND) ∩ (SBC) = KN
(MND) ∩ (SCD) = ND
Vậy thiết diện của mặt phẳng (MND) với hình chóp là tứ giác NDMK.
Đáp án B

Chọn B.
Phương pháp:
Tỉ lệ thể tích của các khối chóp .S ABCD và .S MBCDN bằng tỉ lệ diện tích các đa giác ABCD và MBCDN .
Cách giải:
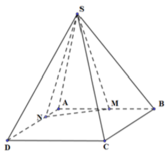
Do các khối chóp .S ABCD và S.MBCDN có cùng chiều cao kẻ từ S nên