cho M =1 trên 22+1 trên 32+1 trên 42+......+1 trên 20142+1 trên 20152
Chứng tỏ rằng giá trị của M không phải là một số tự nhiên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 5 2017
Xét điểm M(x;y;z), N(a;b;c) ta có
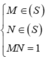
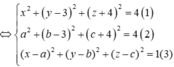
Lấy (1) – (2) theo vế có: 
Kết hợp sử dụng bất đẳng thức Cauchy – Schwarz (Bunhiacopski) và (3) ta có
=-10
Dấu bằng đạt tại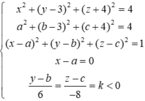 
Chọn đáp án A.
*Một cách tương tự mở rộng cho min –max của α O M 2 + β O N 2 .
24 tháng 7 2017
chọn 6 số bất kì chia thành 2 nhóm 3 số ,từ đó chọn được 2 số âm là a,c . Tổng 30 số còn lại là số âm b. Vậy S=a+b+c là số âm.
Tổng các số trên bảng :
1+2+...+2012+2013=1+2013/2.2013=2027091 là 1 số lẻ.
Mỗi lần xoá 2 số a,b (giả sử a>b) rồi viết vào giá trị tuyệt đối của 2 số(a-b)=a-b sẽ làm tổng các số còn lại trên bảng vẫn là số lẻ. Lặp lại cho đến khi trên bảng còn lại 1 số đó vẫn là số lẻ không thể naò là số 0
CM
6 tháng 10 2019
Đáp án B.
Từ
f x . f ' x = 2 x f 2 x + 1 ⇒ f x . f ' x f 2 x + 1 = 2 x ⇒ ∫ f x . f ' x f 2 x + 1 d x = ∫ 2 x d x
(1)
Đặt
f 2 x + 1 = t ⇒ f 2 x = t 2 − 1 ⇒ 2 f x . f ' x d x = 2 t d t ⇒ f x . f ' x d x = t d t
Suy ra ∫ f x . f ' x f 2 x + 1 x = ∫ t d t t = ∫ d t = t + C 1 = f 2 x + 1 + C 1 và ∫ 2 x d x = x 2 + C 2
Từ (1) ta suy ra f 2 x + 1 + C 1 = x 2 + C 2 . Do f 0 = 0 nên C 2 − C 1 = 1 .
Như vậy
f 2 x + 1 = x 2 + C 2 − C 1 = x 2 + 1 ⇒ f 2 x = x 2 + 1 2 − 1 = x 4 + 2 x 2
⇒ f x = x 4 + 2 x 2 = x x 2 + 2 = x x 2 + 2
(do x ∈ 1 ; 3 ).
Ta có f ' x = x 2 + 2 + x 2 x 2 + 2 = 2 x 2 + 1 x 2 + 2 > 0, ∀ x ∈ ℝ ⇒ Hàm số f x = x x 2 + 2 đồng biến trên R nên f x cũng đồng biến trên 1 ; 3 .
Khi đó M = max 1 ; 3 f x = f 3 = 3 11 và m = min 1 ; 3 f x = f 1 = 3 .
Vậy
P = 2 M − m = 6 11 − 3 ⇒ a = 6 ; b = 1 ; c = 0 ⇒ a + b + c = 7