Cho tỉ thức a/b=c/d chứng minh rằng a+b/c+d tất cả bình phương=a^2+b^2/c^2+d^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk$. Khi đó:
$\frac{ab}{cd}=\frac{bk.b}{dk.d}=\frac{b^2}{d^2}(1)$
$\frac{a^2-b^2}{c^2-d^2}=\frac{(bk)^2-b^2}{(dk)^2-d^2}=\frac{b^2(k^2-1)}{d^2(k^2-1)}=\frac{b^2}{d^2}(2)$
Từ $(1); (2)$ ta có đpcm
------------------------
Lại có:
$(\frac{a+b}{c+d})^2=(\frac{bk+b}{dk+d})^2=(\frac{b(k+1)}{d(k+1)})^2=(\frac{b}{d})^2(3)$
$\frac{a^2+b^2}{c^2+d^2}=\frac{(bk)^2+b^2}{(dk)^2+d^2}=\frac{b^2(k^2+1)}{d^2(k^2+1)}=\frac{b^2}{d^2}=(\frac{b}{d})^2(4)$
Từ $(3); (4)$ ta có đpcm.



Lời giải:
Đặt $\frac{a}{b}=\frac{c}{d}=t\Rightarrow a=bt; c=dt$. Ta có:
$\frac{ab}{cd}=\frac{b^2t}{d^2t}=\frac{b^2}{d^2}(1)$
Mặt khác:
$\frac{(a-b)^2}{(c-d)^2}=\frac{(bt-b)^2}{(dt-d)^2}=\frac{b^2(t-1)^2}{d^2(t-1)^2}=\frac{b^2}{d^2}(2)$
Từ $(1); (2)\Rightarrow \frac{ab}{cd}=\frac{(a-b)^2}{(c-d)^2}$


ta có :
\(\dfrac{a}{b}\)=\(\dfrac{c}{d}\) \(\Rightarrow\) \(\dfrac{a}{c}\) = \(\dfrac{b}{d}\)
đặt \(\dfrac{a}{c}\) = \(\dfrac{b}{d}\) = k \(\Rightarrow\) a = ck ; b = dk
\(\dfrac{ac}{bd}\) = \(\dfrac{ck.c}{dk.d}\) = \(\dfrac{c^2.k}{d^2.k}\) = \(\dfrac{c^2}{d^2}\) (1)
\(\dfrac{a^2+c^2}{b^2+d^2}\) = \(\dfrac{\left(ck\right)^2+c^2}{\left(dk\right)^2+d^2}\) = \(\dfrac{c^2.k^2+c^2}{d^2.k^2+d^2}\) = \(\dfrac{c^2\left(k^2+1\right)}{d^2\left(k^2+1\right)}\) = \(\dfrac{c^2}{d^2}\)(2)
từ (1) , (2) \(\Rightarrow\) \(\dfrac{ac}{bd}\) = \(\dfrac{a^2+c^2}{b^2+d^2}\)
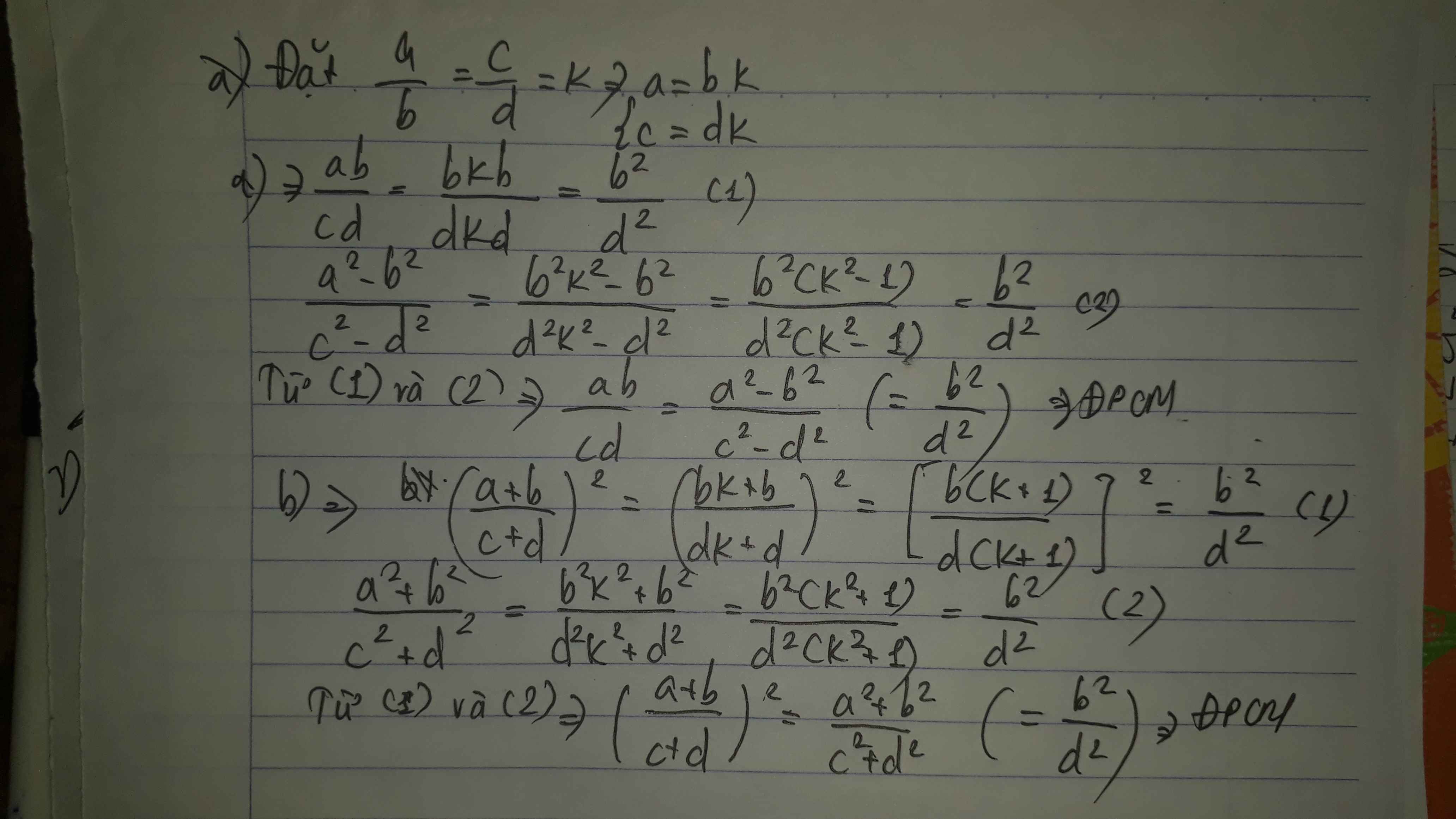
\(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\Leftrightarrow\dfrac{a^2}{c^2}=\dfrac{b^2}{d^2}=\dfrac{a^2+b^2}{c^2+d^2}\)