Điều kiện xác định y>o và x>2

\(\dfrac{5}{x-2}+\dfrac{3}{y}=8\left(1\right)\)

\(\dfrac{2}{x-2}-\dfrac{3}{y}=1\left(2\right)\)

Lấy 1+2 => \(\dfrac{7}{x-2}=9=>7=9.\left(x-2\right)=>x=\dfrac{25}{9}\)(Tm)

Thay x=\(\dfrac{25}{9}\) vào 1 hoặc 2 => \(\dfrac{5}{\dfrac{25}{9}-2}+\dfrac{3}{y}=8=>y=\dfrac{21}{11}\)(TM)

Vậy.........

ĐKXĐ: x<>0; y<>0

\(\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{3}{y}=1\\\dfrac{2}{x}+\dfrac{1}{y}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{3}{y}=1\\\dfrac{6}{x}+\dfrac{3}{y}=-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-\dfrac{1}{x}=4\\\dfrac{2}{x}+\dfrac{1}{y}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{4}\\\dfrac{1}{y}=-1-\dfrac{2}{x}=-1-2:\dfrac{-1}{4}=-1+8=7\end{matrix}\right.\)

=>x=-1/4 và y=1/7

ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\y\ne0\end{matrix}\right.\)

Đặt \(\left\{{}\begin{matrix}a=\dfrac{1}{x}\\b=\dfrac{1}{y}\end{matrix}\right.\) 

Hệ phương trình trở thành \(\left\{{}\begin{matrix}5a+3b=1\\2a+b=-1\end{matrix}\right.\)

 \(\Rightarrow\left\{{}\begin{matrix}b=-1-2a\\5a+3\left(-1-2a\right)=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=-1-2a\\-a-3=1\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}a=-4\\b=-1-2.\left(-4\right)\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=-4\\b=7\end{matrix}\right.\)

Ta có: \(\left\{{}\begin{matrix}a=\dfrac{1}{x}=-4\\b=\dfrac{1}{y}=7\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{4}\left(tm\right)\\y=\dfrac{1}{7}\left(tm\right)\end{matrix}\right.\)

Vậy HPT có nghiệm \(x=-\dfrac{1}{4}\) và \(y=\dfrac{1}{7}\)

a.

ĐKXĐ: \(x\ne\pm y\)

Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x+y}=u\\\dfrac{1}{x-y}=v\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}u+v=2\\2u+3v=5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3u+3v=6\\2u+3v=5\\\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u=1\\v=2-u\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}u=1\\v=1\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x+y}=1\\\dfrac{1}{x-y}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\x-y=1\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=1\\y=0\end{matrix}\right.\)

b.

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x^2-4x+7=x+1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x^2-5x+6=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)

TH1: x + y + z $\ne$ 0

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{y+z+1}$ = $\frac{y}{x+z+2}$ = $\frac{z}{x+y-3}$ = $\frac{x+y+z}{y+z+1+x+z+2+x+y-3}$ 

              = $\frac{x+y+z}{x+y+z+x+y+z}$ = $\frac{x+y+z}{2(x+y+z)}$ = $\frac{1}{2}$ 

⇒ x + y + z = $\frac{1}{2}$

⇒ x + y       = $\frac{1}{2}$ - z

    x + z        = $\frac{1}{2}$ - y

    y + z        = $\frac{1}{2}$ - x

Thay y + z + 1 = $\frac{1}{2}$ - x + 1

⇒ $\frac{x}{\frac{1}{2}-x+1}$ = $\frac{1}{2}$

⇒ 2x = $\frac{1}{2}$ - x + 1

⇒ 2x + x = $\frac{1}{2}$ + 1

⇒  3x   =  $\frac{3}{2}$

⇒   x    = $\frac{1}{2}$

Thay x + z + 2 = $\frac{1}{2}$ - y + 2

⇒ $\frac{y}{\frac{1}{2}-y+2}$ = $\frac{1}{2}$

⇒ 2y = $\frac{1}{2}$ - y + 2

⇒ 2y + y = $\frac{1}{2}$ + 2

⇒   3y  = $\frac{5}{2}$

⇒     y   = $\frac{5}{6}$

Thay x + y - 3 = $\frac{1}{2}$ - z - 3

⇒ $\frac{z}{\frac{1}{2}-z-3}=$\frac{1}{2}$

⇒ 2z = $\frac{1}{2}$ - z - 3

⇒ 2z + z = $\frac{1}{2}$ - 3

⇒  3z  = $\frac{-5}{2}$

⇒   z   = $\frac{-5}{6}$

TH2: x + y + z = 0

⇒ $\frac{x}{y+z+1}$ = $\frac{y}{x+z+2}$ = $\frac{z}{x+y-3}$ = 0

⇒ x = y = z = 0

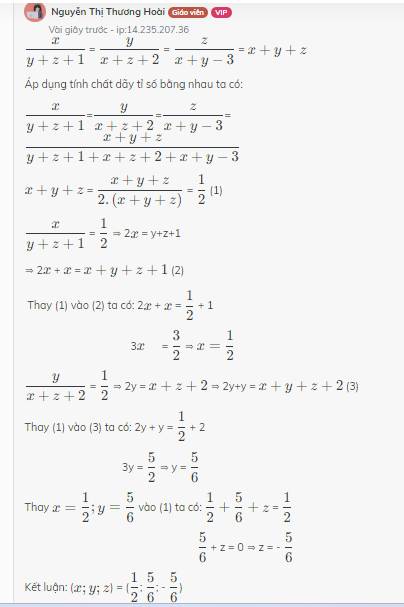
https://olm.vn/cau-hoi/tim-tat-ca-cac-so-xyz-biet-dfracxyz1dfracyxz2dfraczxy-3xyz-giair-chi-tiet-ho-e-vs-a.8297156371934

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x-1+2}{x-1}-\dfrac{5y+10-10}{y+2}=9\\\dfrac{2}{x-1}-\dfrac{5}{y+2}=4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x-1}+1-5+\dfrac{10}{y+2}=9\\\dfrac{2}{x-1}-\dfrac{5}{y+2}=4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x-1}+\dfrac{10}{y+2}=9+5-1=14-1=13\\\dfrac{2}{x-1}-\dfrac{5}{y+2}=4\end{matrix}\right.\)

=>x-1=2/7; y+2=5/3

=>x=9/7; y=-1/3

ĐK:   \(x\ne0\) ; \(y\ne0\)

Hệ phương trình tương đương với:

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+\dfrac{1}{x}\right)+\left(y+\dfrac{1}{y}\right)=4\\\left(x+\dfrac{1}{x}\right)^2+\left(y+\dfrac{1}{y}\right)^2=8\end{matrix}\right.\)

Đặt  \(S=\left(x+\dfrac{1}{x}\right)+\left(y+\dfrac{1}{y}\right)\)

         \(P=\left(x+\dfrac{1}{x}\right)\left(y+\dfrac{1}{y}\right)\)

Mà   \(S^2\ge4P\)

Ta có:      \(\left\{{}\begin{matrix}S=4\\S^2-2P=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S=4\\P=4\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}\left(x+\dfrac{1}{x}\right)+\left(y+\dfrac{1}{y}\right)=4\\\left(x+\dfrac{1}{x}\right)\left(y+\dfrac{1}{y}\right)=4\end{matrix}\right.\)

⇔ \(\left\{{}\begin{matrix}x+\dfrac{1}{x}=2\\y+\dfrac{1}{y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)

bạn làm thế nào đẻ ghi được hệ vậy, chỉ mình vói sau đó minh se viet loi giai cho bạn

trên chỗ trả lời có chỗ ghi hệ mà bạn (cạnh lệnh TEX ý) rồi bạn chọn lệnh thứ 4 từ phải qua trái rồi bạn chọn số pt trong hệ pt và điền vô thôi :v (mình không biết edit ảnh nên chắc bạn khó hiểu)