Để giải phương trình xy + 2x - y = 9, ta có thể sử dụng phương pháp hoán vị.

Đặt u = x - 1 và v = y + 2, ta có:

(u + 1)(v - 2) + 2(u + 1) - (v - 2) = 9

Mở ngoặc và đơn giản hóa, ta được:

uv + u + 2v - 4 + 2u + 2 - v + 2 = 9

Kết hợp các thành phần tương tự, ta có:

uv + 3u + v = 9

Thêm 3 cả hai vế của phương trình, ta có:

uv + 3u + v + 3 = 12

Nhân cả hai vế của phương trình với 4, ta có:

4uv + 12u + 4v + 12 = 48

Nhóm các thành phần tương tự, ta có:

(4u + 1)(v + 3) = 48

Ta cần tìm các cặp giá trị nguyên dương (u, v) sao cho (4u + 1)(v + 3) = 48.

Các cặp giá trị nguyên dương (u, v) thỏa mãn phương trình trên là:

(1, 45), (3, 15), (5, 9), (9, 5), (15, 3), (45, 1)

Quay lại định nghĩa của u và v, ta có:

x - 1 = u → x = u + 1

y + 2 = v → y = v - 2

Vậy, các cặp giá trị nguyên dương (x, y) thỏa mãn phương trình ban đầu là:

(2, 43), (4, 13), (6, 7), (10, 3), (16, 1), (46, -1)

Tuy nhiên, để thỏa mãn y ∈ N, ta chỉ lấy các giá trị y là số tự nhiên dương.

Vậy, các cặp giá trị nguyên dương (x, y) thỏa mãn phương trình ban đầu là:

(6, 7), (10, 3)

xy+2x-y=9

=>x(y+2)-y-2=7

=>x(y+2)-(y+2)=7

=>(x-1)(y+2)=7

\(\Leftrightarrow\left(x-1;y+2\right)\in\left\{\left(1;7\right);\left(7;1\right);\left(-1;-7\right);\left(-7;-1\right)\right\}\)

=>\(\left(x,y\right)\in\left\{\left(2;5\right);\left(8;-1\right);\left(0;-9\right);\left(-6;-3\right)\right\}\)

mà x,y đều là số tự nhiên

nên \(\left(x,y\right)\in\left(2;5\right)\)

hình như sai giả thiết

bài 1 : a,ta có 3/x-1 =4/y-2=5/z-3 =>  x-1/3=y-2/4=z-3/5 

áp dụng .... => x-1+y-2+z-3 / 3+4+5 = x+y+z-1-2-3/3+4+5 = 12/12=1

do x-1/3 = 1 => x-1 = 3 => x= 4 ( tìm y,z tương tự

Bài 1: 

a) Ta có: 3/x - 1 = 4/y - 2 = 5/z - 3 => x - 1/3 = y - 2/4 = z - 3/5 áp dụng ... =>x - 1 + y - 2 + z - 3/3 + 4 + 5 = x + y + z - 1 - 2 - 3/3 + 4 + 5 = 12/12 = 1 do x - 1/3 = 1 => x - 1 = 3 => x = 4 ( tìm y, z tương tự )

a) Áp dụng tính chất dãy tỉ số bằng nhau ta được:

X/3 = y/4 = x/3 + y/4 = 28/7 = 4

=> x = 4 × 3 = 12

=> y = 4 × 4 = 16

Vậy x = 12, y = 16

B) Áp dụng tính chất dãy tỉ số bằng nhau ta được:

X/2 = y/(-5) = x/2 - y/(-5) = (-7)/7 = -1

=> x = -1 × 2 = -2

=> y = -1 × -5 = 5

Vậy x = -2, y = 5

C) làm tương tự như bài a, b

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

Do đó: x=16; y=24; z=30

y = 57

y = 91/9

Y × 4 + 6 × Y = 570

Y × ( 4 + 6 ) = 570

Y × 10 = 570 

Y          = 570 : 10

Y          = 57 

Y × 5 +  4 × Y = 918 

Y × ( 5 + 4 ) = 918 

Y  ×   9 = 918

Y           = 918 : 9 

Y           =  102 

Đặt \(\dfrac{x}{y}+\dfrac{y}{x}=t\Rightarrow\left|t\right|\ge2\)

\(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}=t^2-2\)

\(\dfrac{x^4}{y^4}+\dfrac{y^4}{x^4}=\left(\dfrac{x^2}{y^2}+\dfrac{y^2}{x^2}\right)^2-2=\left(t^2-2\right)^2-2=t^4-4t^2+2\)

\(\Rightarrow P=f\left(t\right)=t^4-4t^2+2-\left(t^2-2\right)+t\)

\(f\left(t\right)=t^4-5t^2+t+4\)

Xét hàm \(f\left(t\right)=t^4-5t^2+t+4\) trên \((-\infty;-2]\cup[2;+\infty)\)

\(f'\left(t\right)=g\left(t\right)=4t^3-10t+1\)

\(g\left(t\right)\) bậc 3 nên có tối đa 3 nghiệm

\(g\left(-2\right)=-11\) ; \(g\left(0\right)=1\)

\(\Rightarrow g\left(-2\right).g\left(0\right)< 0\Rightarrow g\left(t\right)=0\) có nghiệm \(t_1\in\left(-2;0\right)\)

\(g\left(1\right)=-5< 0\Rightarrow g\left(0\right).g\left(1\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_2\in\left(0;1\right)\)

\(g\left(2\right)=13\Rightarrow g\left(1\right).g\left(2\right)< 0\Rightarrow g\left(t\right)\) có nghiệm \(t_3\in\left(1;2\right)\)

Dấu \(f'\left(t\right)\):

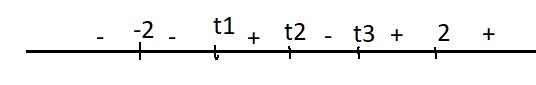
Từ đây ta thấy \(f\left(t\right)\) nghịch biến trên \((-\infty;-2]\) và đồng biến trên \([2;+\infty)\)

Hay GTNN của \(f\left(t\right)\) sẽ rơi vào \(t=-2\) hoặc \(t=2\)

\(f\left(-2\right)=-2\) ; \(f\left(2\right)=2\)

\(\Rightarrow f\left(t\right)_{min}=-2\) khi \(t=-2\) hay \(P_{min}=-2\) khi \(x=-y\)

a) (y - 24) : 28 = 20

y - 24 = 20 x 28

y - 24 = 560 

y = 560 + 24 

y = 584

vậy y = ...

a. 

\(\left(y-24\right):28=20\)

\(\left(y-24\right)=560\)

\(y=584\)

b. \(13\times\left(y-6\right)=4\times y-6\)

\(13\times y-78=4\times y-6\)

\(9\times y=72\)
\(y=8\)
c.\(y\times3+y\times4+y:3+y:4=182\)

\(y\times\left(3+4\right)+y:\left(3+4\right)=182\)

\(y\times\left(7+\dfrac{1}{7}\right)=182\)

\(y=\dfrac{637}{25}\)

B nha em

Chọn B