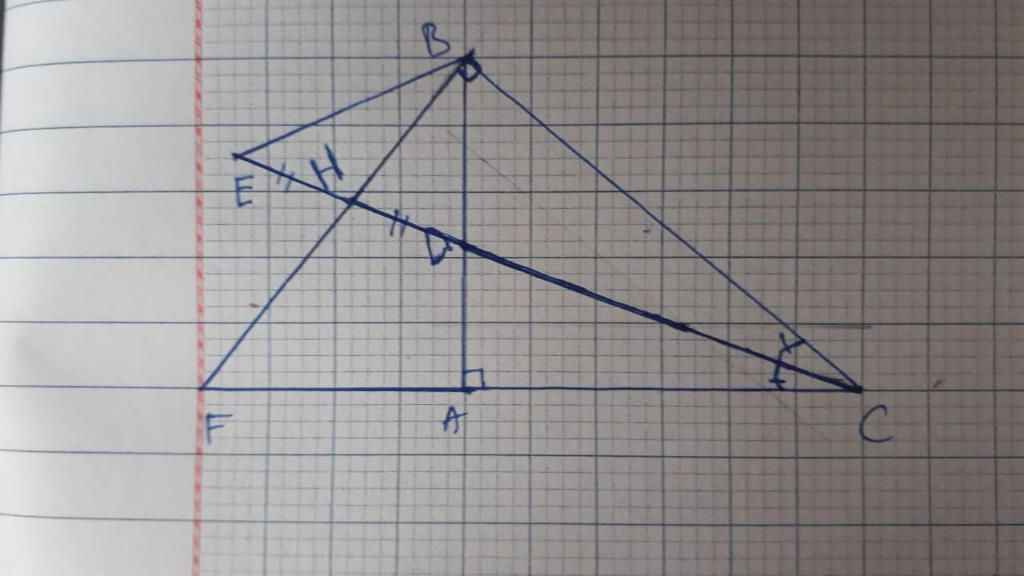
a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE

a) Xét ΔBDH vuông tại H và ΔBEH vuông tại H có 

BH chung

DH=EH(H là trung điểm của DE)

Do đó: ΔBDH=ΔBEH(hai cạnh góc vuông)

Suy ra: \(\widehat{BDH}=\widehat{BEH}\)(hai góc tương ứng)

mà \(\widehat{BDH}=\widehat{ADC}\)(hai góc đối đỉnh)

và \(\widehat{CEB}=\widehat{BEH}\)

nên \(\widehat{CEB}=\widehat{ADC}\)(đpcm)

Ta có: ΔBDH=ΔBEH(cmt)

nên \(\widehat{DBH}=\widehat{EBH}\)(hai góc tương ứng)(1)

Xét ΔADC vuông tại A và ΔHDB vuông tại H có 

\(\widehat{ADC}=\widehat{HDB}\)(hai góc đối đỉnh)

Do đó: ΔADC\(\sim\)ΔHDB(g-g)

Suy ra: \(\widehat{ACD}=\widehat{HBD}\)(hai góc tương ứng)(2)

Từ (1) và (2) suy ra \(\widehat{EBH}=\widehat{ACD}\)(Đpcm)

a,△BED có H là trung điểm của DE và BH ┴ DE 
=> △BED cân ở B 
=> ∠BED = ∠BDE 
∠BDE = ∠ADC (đối đỉnh) 
=> ∠BED = ∠ADC 
△BED cân ở B => BH là phân giác của ∠EBD 
=> ∠EHB = ∠DBH 
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD 
=> ∠EBH = ∠ACD 
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB) 
= 90⁰ - ∠CBH 
=> ∠EHB + ∠CBH = 90⁰ 
=> BE ┴ BC 
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D} 
=> D là trực tâm của △FBC 
=> FD ┴ BC 
BE ┴ BC 
=> FD//BE 

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
 => BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE. 
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
 =>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
 (Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của  ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE      => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực  Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/

(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
 => ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM          => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của  ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).

a,\(\Delta\)BED có H là trung điểm của DE và BH \(\perp\) DE 
=> \(\Delta\)BED cân ở B 
=> Góc BED = Góc BDE 
Góc BDE = Góc ADC (đối đỉnh) 
=> Góc BED = Góc ADC 
\(\Delta\)BED cân ở B => BH là phân giác của góc EBD 
=> gócEHB = gócDBH 
mà gócDBH = 90⁰ - gócBFA = 90⁰ - gócHFC = gócACD 
=> gócEBH = gócACD 
b, gócEBH = gócACD = gócDCB (vì CH là phân giác của gócACB) 
= 90⁰ - gócCBH 
=> gócEHB + gócCBH = 90⁰ 
=> BE \(\perp\) BC 
c, △FBC có CH \(\perp\) BF ; BA \(\perp\) FC ; CH \(\cap\) BA = D 
=> D là trực tâm của \(\Delta\)FBC 
=> FD \(\perp\) BC 
BE \(\perp\) BC 
=> FD//BE 

1) a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE