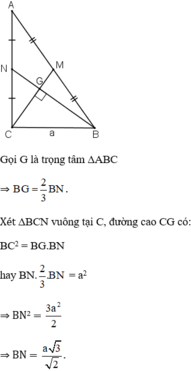
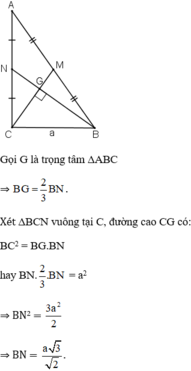
Gọi giao điểm của BN, CM là G => G là trọng tâm của tam giác ABC

Ta có: BN vuông góc vs CM

=> BG vuông góc vs GM và CG vuông góc vs GN

=> MG² + GB² = BM² =(1/2.AB)² =90,25 và CG² + GN² = NC² = (1/2AC)² = 121 (ĐL Pytago)

=> MG² + GB² + CG² + GN² = 211,25

Mà MG = 1/2 CG và NG = 1/2 BG (Vì G là trọng tâm)

=> (1/2CG)² + CG² + (1/2 BG)²  + BG² =211,25 => 5/4 BG² + 5/4 CG² =211,25

=> BG² +CG² = 211,25 : 5/4 =169

=> BC² = 169 (Vì BG² +CG² = BC²) => BC = 13

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC

 => AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.

Tam giác ANB vuông tại A có AN²+AB²=BN² (Theo Pytago)   mà BN=9cm (gt)

=>AN²+AB²=81        Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC²+AB²=81     (1)

Tam giác ABC vuông tại A có: AC²+AB²=BC² => BC² - AB² = AC²   (2)

Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC² - AB²)+AB²=81       mà BC=12(cmt)

=> 36 - \(\frac{1}{4}\)AB²+AB²=81

=> 36+\(\frac{3}{4}\)AB²=81

=> AB²=60=>AB=\(\sqrt{60}\)

C2

Cho hình thang cân ABCD có đáy lớn CD = 1

C4

Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath

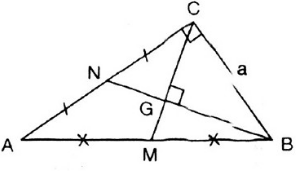
a; DN\(\perp\)AC

AB\(\perp\)AC

Do đó: DN//AB

=>DN//MB

Xét tứ giác BMND có

BM//DN

BD//MN

Do đó: BMND là hình bình hành

b: Xét ΔABC có

N là trung điểm của AC

NM//BC

Do đó: M là trung điểm của AB

Xét ΔABC có

M,N lần lượt là trung điểm của AB,AC

=>MN là đường trung bình của ΔABC

=>\(MN=\dfrac{BC}{2}=\dfrac{10}{2}=5\left(cm\right)\)

còn câu c thì làm ntn