Cho đường tròn (O) và điểm I không nằm trên (O). Từ điểm I kẻ hai dây cung AB và CD ( A nằm giữa I và B; C nằm giữa I và D ) a, So sánh các cặp góc ACI và ABD, CAI và CDB b, CM tam giác IAC đồng dạng với tam giác IDB c, CM IA.IB = IC.ID
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
1 tháng 4 2019
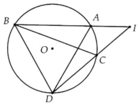
a, HS tự chứng minh
b, ∆IAC:∆IDB (g.g)
c, Sử dụng kết quả câu b)

16 tháng 8 2021
Xét (O) có
\(\widehat{AEB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{AEB}=90^0\)
Xét tứ giác BEFI có
\(\widehat{BEF}+\widehat{FIB}=180^0\)
nên BEFI là tứ giác nội tiếp
hay B,E,F,I cùng thuộc 1 đường tròn

LM
Lê Minh Vũ
CTVHS
16 tháng 8 2021
a) \(\Delta ABE\)nội tiếp đường tròn đường kính \(AB\)
\(\Rightarrow\)\(\Delta ABE\perp E\)
\(\Rightarrow\)\(AEB\lambda=90\)độ
Tứ giác\(BEFI\)nội tiếp đường tròn đường kính \(FB\)




a) So sánh \(\widehat{ACI}\) và \(\widehat{ABD}\) và cặp góc \(\widehat{CAI}\) và \(\widehat{CDB}\)
Ta có \(\widehat{ACI}+\widehat{ACD}=180^o\) (hai góc kề bù) \(\left(1\right)\)
Xét \(\left(O\right)\) có:
\(\widehat{ABD}\) là góc nối tiếp chắn cung \(AD\)
\(\widehat{ACD}\) là góc nối tiếp chắn cung \(AD\)
\(\Rightarrow\widehat{ABD}+\widehat{ACD}=\dfrac{1}{2}.360^o=180^o\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ⇔ \(\widehat{ACI}=\widehat{ABD}=180^o-\widehat{ACD}\)
Ta có: \(\widehat{CAI}+\widehat{BAC}=180^o\) (hai góc kề bù)
Xét \(\left(O\right)\) có:
\(\widehat{BAC}\) là góc nội tiếp của chắn cung \(BC\)
\(\widehat{CDB}\) là góc nội tiếp của chắn cung \(BC\)
\(\Rightarrow\widehat{BAC}+\widehat{CDB}=\dfrac{1}{2}.360^o=180^o\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\widehat{CAI}=\widehat{CDB}=180^o-\widehat{BAC}\)
b) Chứng minh tam giác IAC đồng dạng với tam giác IDB
Xét \(\Delta IAC\) và \(\Delta IDB\) có:
\(\widehat{A}\) là góc chung
\(\widehat{IAC}=\widehat{IDB}\) (câu a)
\(\Rightarrow\Delta IAC\sim\Delta IDB\)
c) Chứng minh \(IA.IB=IC.ID\)
Theo câu b ta có \(\Delta IAC\sim\Delta IDB\)
Suy ra: \(\dfrac{IA}{ID}=\dfrac{IC}{IB}\)
Hay: \(IA.IB=IC.ID\) (đpcm)
a: ACDB là tứ giác nội tiếp
=>góc ABD+góc ACD=180 độ;góc BAC+góc BDC=180 độ
=>góc ACI=góc ABD;góc CAI=góc CDB
b: Xét ΔIAC và ΔIDB có
góc IAC=góc IDB
góc AIC chung
=>ΔIAC đồng dạg với ΔIDB
c: ΔIAC đồng dạng vơi ΔIDB
=>IA/ID=IC/IB
=>IA*IB=IC*ID