a) Phương trình bậc hai

2 x 2   –   7 x   +   3   =   0

Có: a = 2; b = -7; c = 3;

Δ   =   b 2   –   4 a c   =   ( - 7 ) 2   –   4 . 2 . 3   =   25   >   0

Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:

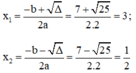
Vậy phương trình có hai nghiệm là 3 và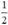 

b) Phương trình bậc hai  6 x 2   +   x   +   5   =   0

Có a = 6; b = 1; c = 5; 

Δ   =   b 2   –   4 a c   =   12   –   4 . 5 . 6   =   - 119   <   0

Vậy phương trình vô nghiệm.

c) Phương trình bậc hai  6 x 2   +   x   –   5   =   0

Có a = 6; b = 1; c = -5;

Δ   =   b 2   –   4 a c   =   12   –   4 . 6 . ( - 5 )   =   121   >   0

Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:

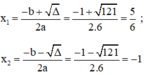
Vậy phương trình có hai nghiệm là -1 và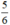 

d) Phương trình bậc hai  3 x 2   +   5 x   +   2   =   0

Có a = 3; b = 5; c = 2;

Δ   =   b 2   –   4 a c   =   5 2   –   4 . 3 . 2   =   1   >   0

Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:

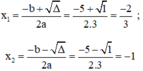
Vậy phương trình có hai nghiệm là -1 và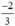 

e) Phương trình bậc hai  y 2   –   8 y   +   16   =   0

Có a = 1; b = -8; c = 16;  Δ   =   b 2   –   4 a c   =   ( - 8 ) 2   –   4 . 1 . 16   =   0 .

Áp dụng công thức nghiệm ta có phương trình có nghiệm kép :

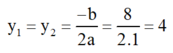
Vậy phương trình có nghiệm kép y = 4.

f) Phương trình bậc hai  16 z 2   +   24 z   +   9   =   0

Có a = 16; b = 24; c = 9;  Δ   =   b 2   –   4 a c   =   24 2   –   4 . 16 . 9   =   0

Áp dụng công thức nghiệm ta có phương trình có nghiệm kép:

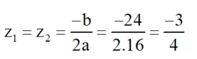
Vậy phương trình có nghiệm kép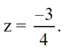 

Kiến thức áp dụng

Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.

+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt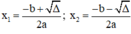 

+ Nếu Δ = 0, phương trình có nghiệm kép  ;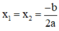

+ Nếu Δ < 0, phương trình vô nghiệm.

\(x^4-9x^2+24x-16=\)\(0\)

\(\Leftrightarrow x^4-\left(9x^2-24x+16\right)=0\)

\(\Leftrightarrow x^4-\left(3x-4\right)^2=0\)

\(\Leftrightarrow\left(x^2+3x-4\right)\left(x^2-3x+4\right)=0\)

\(\Leftrightarrow\left(x+4\right)\left(x-1\right)\left[\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\right]=0\)

Vì \(\left(x-\frac{3}{2}\right)^2+\frac{7}{4}>0\forall x\)nên:

\(\left(x+4\right)\left(x-1\right)=0:\left[\left(x-\frac{3}{2}\right)^2+\frac{7}{4}\right]\)

\(\Leftrightarrow\left(x+4\right)\left(x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\x-1=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-4\\x=1\end{cases}}\)

Vậy phương trình có tập nghiệm \(S=\left\{1;-4\right\}\)

\(x^4=6x^2+12x+\)\(8\)

\(\Leftrightarrow x^4-2x^2+1=4x^2+12x+9\)

\(\Leftrightarrow\left(x^2-1\right)^2=\left(2x+3\right)^2\)

\(\Leftrightarrow|x^2-1|=|2x+3|\)\(|\)

xét các trường hợp:

- Trường hợp 1:

\(x^2-1=2x+3\)

\(\Leftrightarrow x^2-1-2x-3=0\)

\(\Leftrightarrow x^2-2x-4=0\)

\(\Leftrightarrow\left(x-1\right)^2-5=0\Leftrightarrow\left(x-1\right)^2=5\)

\(\Leftrightarrow\orbr{\begin{cases}x-1=\sqrt{5}\\x-1=-\sqrt{5}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1+\sqrt{5}\\x=1-\sqrt{5}\end{cases}}}\)

-Trường hợp 2:

\(x^2-1=-2x-3\)

\(\Leftrightarrow x^2-1+2x+3=0\)

\(\Leftrightarrow x^2+2x+2=0\)

\(\Leftrightarrow\left(x+1\right)^2+1=0\)

\(\Leftrightarrow\left(x+1\right)^2=-1\left(vn\right)\)(vô nghiệm)

Vậy phương trình có tập nghiệm: \(S=\left\{1\pm\sqrt{5}\right\}\)

ĐKXĐ: \(x\ge1\).

Phương trình đã cho tương đương:

\(\sqrt{x+3}+\sqrt{x-1}=\dfrac{8}{\sqrt{4x^4-12x^3+9x^2+16}-\left(2x^2-3x\right)}\)

\(\Leftrightarrow\sqrt{x+3}+\sqrt{x-1}=\dfrac{\sqrt{4x^4-12x^3+9x^2+16}+\left(2x^2-3x\right)}{2}\)

\(\Leftrightarrow\sqrt{4x^4-12x^3+9x^2+16}+\left(2x^2-3x\right)-2\sqrt{x+3}-2\sqrt{x-1}=0\)

\(\Leftrightarrow\left(\sqrt{4x^4-12x^3+9x^2+16}-2\sqrt{x+3}\right)+\left(2x^2-3x-2\sqrt{x-1}\right)=0\)

\(\Leftrightarrow\dfrac{4x^4-12x^3+9x^2-4x+4}{\sqrt{4x^4-12x^3+9x^2+16}+2\sqrt{x+3}}+\dfrac{4x^4-12x^3+9x^2-4x+4}{2x^2-3x+2\sqrt{x-1}}=0\)

\(\Leftrightarrow\left(x-2\right)\left(4x^3-4x^2+x-2\right)\left(\dfrac{1}{\sqrt{4x^4-12x^3+9x^2+16}+2\sqrt{x+3}}+\dfrac{1}{2x^2-3x+2\sqrt{x-1}}\right)=0\).

Do \(x\ge1\) nên ta có \(\dfrac{1}{\sqrt{4x^4-12x^3+9x^2+16}+2\sqrt{x+3}}+\dfrac{1}{2x^2-3x+2\sqrt{x-1}}>0\).

Do đó \(\left[{}\begin{matrix}x-2=0\Leftrightarrow x=2\left(TMĐK\right)\\4x^3-4x^2+x-2=0\left(1\right)\end{matrix}\right.\).

Giải phương trình bậc 3 ở (1) ta được \(x=\dfrac{\sqrt[3]{36\sqrt{13}+53\sqrt{6}}}{\sqrt[6]{279936}}+\dfrac{1}{\sqrt[6]{7776}\sqrt[3]{36\sqrt{13}+53\sqrt{6}}}+\dfrac{1}{3}\approx1,157298106\left(TMĐK\right)\).

Vậy...

Vì trong bài làm của mình có một số dòng khá dài nên bạn có thể vào trang cá nhân của mình để đọc tốt hơn!

a) Ta có: \(x^3-9x^2+19x-11=0\)

\(\Leftrightarrow x^3-x^2-8x^2+8x+11x-11=0\)

\(\Leftrightarrow x^2\left(x-1\right)-8x\left(x-1\right)+11\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2-8x+11\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x^2-8x+11=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\sqrt{5}+4\\x=-\sqrt{5}+4\end{matrix}\right.\)

Vậy: \(S=\left\{1;\sqrt{5}+4;-\sqrt{5}+4\right\}\)

\(x^3-2\sqrt{2}x^2+6x-4\sqrt{2}=0\)

\(\Leftrightarrow\left(x^3-\sqrt{2}x^2+4x\right)-\left(\sqrt{2}x^2+2x-4\sqrt{2}\right)=0\)

\(\Leftrightarrow x\left(x-\sqrt{2}x+4\right)-\sqrt{2}\left(x-\sqrt{2}x+4\right)=0\)

\(\Leftrightarrow\left(x-\sqrt{2}\right)\left(x^2-\sqrt{2}x+4\right)=0\)

\(\Leftrightarrow x=\sqrt{2}\)

Bài 1: 

a: \(\Leftrightarrow x^2-5x+6< =0\)

=>(x-2)(x-3)<=0

=>2<=x<=3

b: \(\Leftrightarrow\left(x-6\right)^2< =0\)

=>x=6

c: \(\Leftrightarrow x^2-2x+1>=0\)

\(\Leftrightarrow\left(x-1\right)^2>=0\)

hay \(x\in R\)

a)
=(x-2)³
b)\(\left(2-x\right)^3\)
c)\(\left(x+\dfrac{1}{3}\right)^3\)
d)\(\left(\dfrac{x}{2}+y\right)^3\)
e)
\(=\left(x-1\right)^2\left(x-1-15\right)+25\left[3\left(x-1\right)-5\right]\)
\(=\left(x-1\right)^2\left(x-16\right)+25\left(3x-3-5\right)\)
\(=\left(x-1\right)^2\left(x-16\right)+25\left(3x-8\right)\)
 

- đợi mk 6s hoàn thiện

x⁴ + 5x³ + 12x² + 20x + 16 = 0 

Nhận xét: vì 16/1 = (20/5)² ⇒ đây là pt đối xứng. Vì x = 0 không là nghiệm của pt nên chia 2 vế của pt cho x²⇒pt trở thành: 

⇔x² + 5x + 12+ 20/x + 16/x² = 0 

⇔(x²+ 16/x²) +5(x+4/x) + 12 = 0 

đặt x+4/x = t ⇒ t² = x²+ 8 + 16/x² 

học tốt!

A

A. (x-2)³ = x³ - 6x² +12x - 8 (hằng đẳng thức)