1) Quan sát hình dưới đây
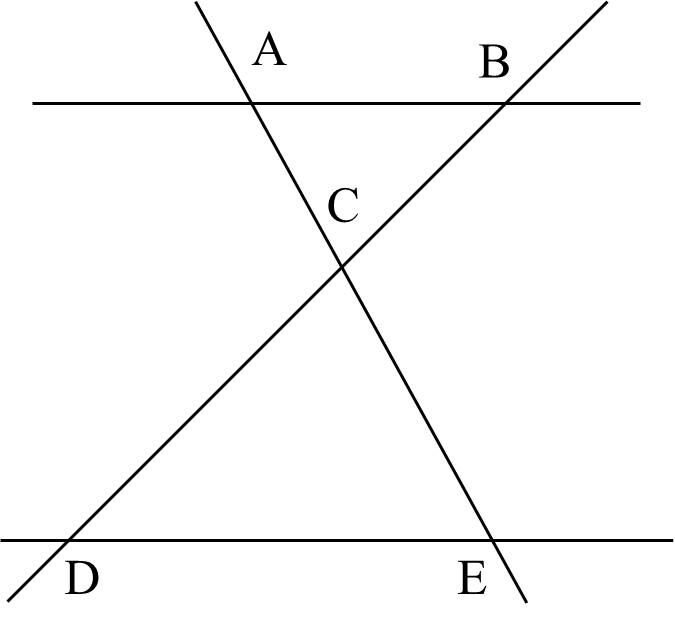
a) Chỉ ra các điểm thuộc đoạn thẳng $BD$, các điểm không thuộc đoạn thẳng $BD$. (0,25 điểm).
b) Chỉ ra các cặp đường thẳng song song. (0,25 điểm).
c) Chỉ ra các cặp đường thẳng cắt nhau và xác định giao điểm của chúng. (0,5 điểm).
2) Cho hai điểm phân biệt $A$ và $B$ cùng nằm trên tia $O x$ sao cho $O A=4 $ cm, $O B=6 $ cm. Gọi $M$ là trung điểm của đoạn thẳng $A B$. Tính độ dài đoạn thẳng $O M$.


Theo đề ra, ta có:
\(AB=OB-OA=6-4=2cm\)
\(\Rightarrow AM=\dfrac{AB}{2}=\dfrac{2}{2}=1cm\)
\(OM=OA+AM=4+1=5cm\).
a) Tập hợp các điểm thuộc đoạn thẳng ��BD là �;�;�B;C;D, tập hợp các điểm thuộc không đoạn thẳng ��BD là �;�A;E.
b) Cặp đường thẳng song song là ��AB // ��DE.
c) Gợi ý: Liệt kê theo các giao điểm, có 5 giao điểm nên có 5 cặp đường thẳng cắt nhau.
Các cặp đường thẳng cắt nhau là
��AB và ��AE cắt nhau tại �A.
��BA và ��BD cắt nhau tại �B.
��AE và ��BD cắt nhau tại �C.
��DE và ��DB cắt nhau tại �D.
��EA và ��ED cắt nhau tại �E.
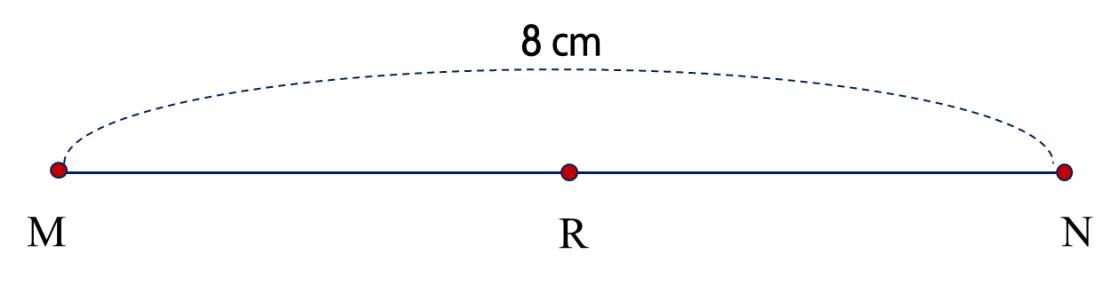
2)
a)
Vì �R là trung điểm của đoạn thẳng ��MN, nên ta có ��=��=��:2MR=RN=MN:2.
Độ dài của đoạn thẳng ��MR hay ��RN là:
8:2=48:2=4 (cm)
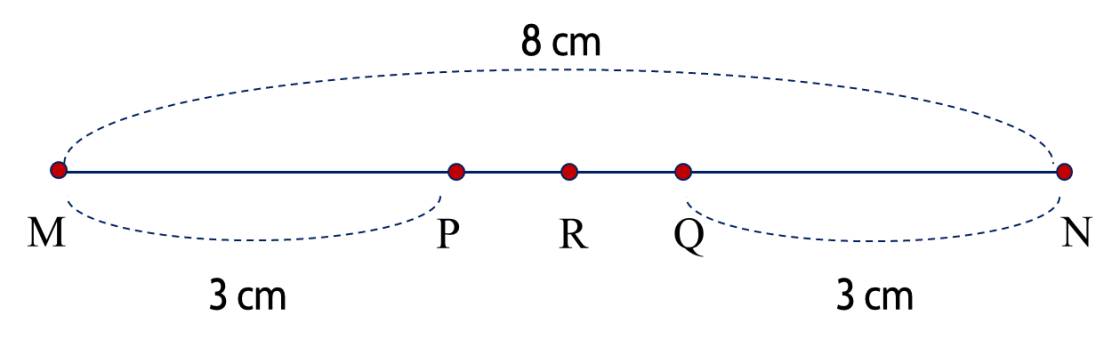
b)
Nhìn hình vẽ, ta thấy �R nằm giữa �P và �Q; ��=��+��+��MN=MP+PQ+QN; ��=��+��MR=MP+PR.
Độ dài của đoạn thẳng ��PQ là
8−3−3=28−3−3=2 (cm).
Độ dài của đoạn thẳng ��PR là
4−3=14−3=1 (cm).
Từ đây, ta thấy ��:��=12PR:PQ=21,
Vậy �R là trung điểm ��PQ.
3)