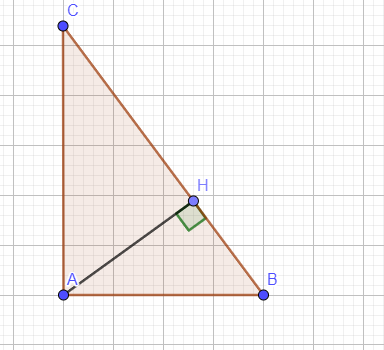
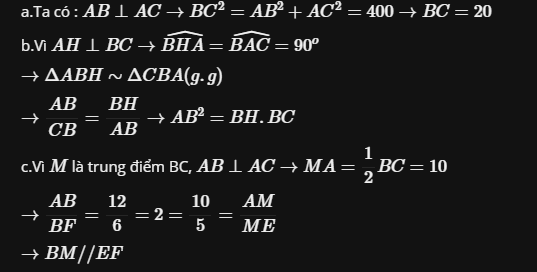Cho ΔABC, đường cao AH
Chứng minh:
a)ΔABCᔕΔHBA, AB2=BH*BC
b)AC2=CH*BC
c)AH2=BH*CH
d)\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
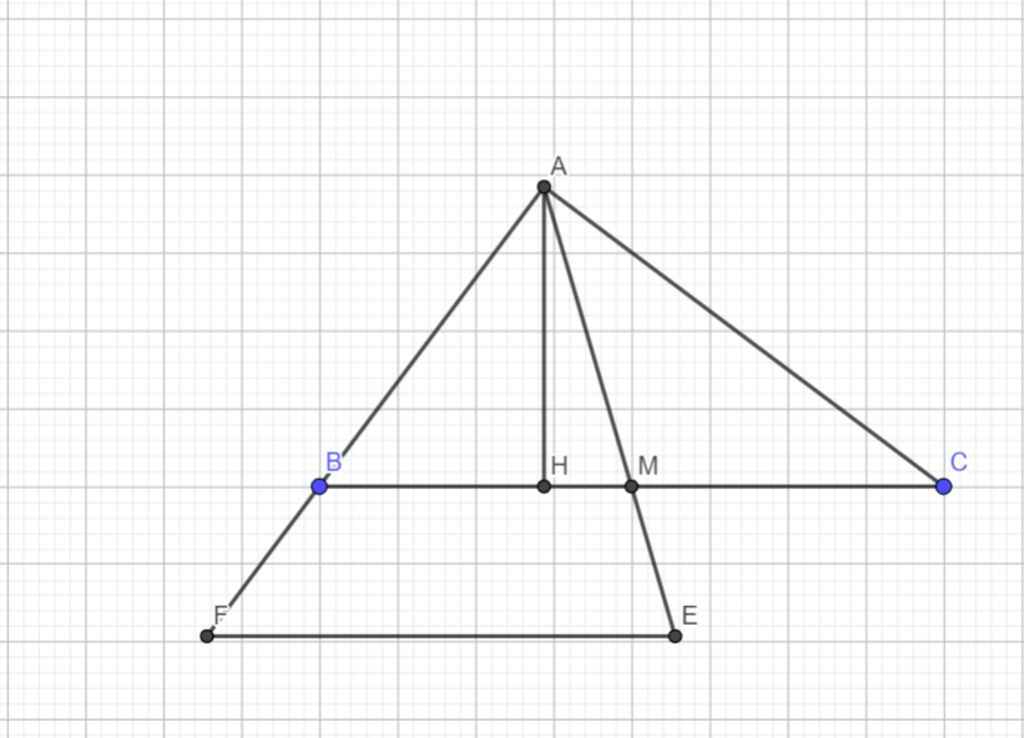
e)Biết M ∈ tia đối tia AC, AM<AC
AE⊥BM tại E
Chứng minh góc BEH=góc BAH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) \(\widehat{BDE}=90^0-\widehat{CDE}=\widehat{BCE}\)
\(\Rightarrow\)△BDE∼△DCE (g-g) \(\Rightarrow\dfrac{BE}{DE}=\dfrac{DE}{CE}\Rightarrow BE.CE=DE^2\left(1\right)\)
-△AHC có: AH//DE (cùng vuông góc BC) \(\Rightarrow\dfrac{DE}{AH}=\dfrac{CE}{CH}\Rightarrow DE=\dfrac{CE.AH}{CH}\Rightarrow DE^2=\dfrac{AH^2.CE^2}{CH^2}\left(2\right)\)
-Từ (1) và (2) ta có điều cần phải c/m.

Ta có: \(\dfrac{AB}{AC}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{1}{16}\)
hay HC=16HB
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow16HB^2=148\)
\(\Leftrightarrow HB=\dfrac{\sqrt{37}}{2}\)
\(\Leftrightarrow HC=8\sqrt{37}\)
\(\Leftrightarrow BC=\dfrac{17\sqrt{37}}{2}\left(cm\right)\)

a) Ta có: \(\angle HEA=\angle HFA=\angle EAF=90\Rightarrow AEHF\) là hình chữ nhật
\(\Delta AHB\) vuông tại H có HE là đường cao \(\Rightarrow AE.AB=AH^2\)
\(\Delta AHC\) vuông tại H có HF là đường cao \(\Rightarrow AF.AC=AH^2\)
\(\Rightarrow AE.AB=AF.AC\)
b) \(\Delta ABC\) vuông tại A có đường cao AH \(\Rightarrow\left\{{}\begin{matrix}AB^2=BH.BC\\AC^2=CH.BC\end{matrix}\right.\)
\(\Rightarrow AB^2-AC^2=BH.BC-CH.BC=BC\left(BH-CH\right)\)
\(=\left(BH+CH\right)\left(BH-CH\right)=BH^2-CH^2\)
c) Ta có: \(\dfrac{1}{HF^2}-\dfrac{1}{CH^2}=\dfrac{1}{AF.FC}-\dfrac{1}{CA.CF}=\dfrac{1}{CF}\left(\dfrac{1}{AF}-\dfrac{1}{CA}\right)\)
\(=\dfrac{1}{CF}.\dfrac{CF}{AF.AC}=\dfrac{1}{AH^2}\)
Lại có: \(\dfrac{1}{HE^2}-\dfrac{1}{BH^2}=\dfrac{1}{BE.EA}-\dfrac{1}{BE.BA}=\dfrac{1}{BE}\left(\dfrac{1}{EA}-\dfrac{1}{BA}\right)\)
\(=\dfrac{1}{BE}.\dfrac{BE}{EA.BA}=\dfrac{1}{AH^2}\)
\(\Rightarrow\dfrac{1}{HF^2}-\dfrac{1}{CH^2}=\dfrac{1}{HE^2}-\dfrac{1}{BH^2}\Rightarrow\dfrac{1}{BH^2}-\dfrac{1}{CH^2}=\dfrac{1}{HE^2}-\dfrac{1}{HF^2}\)
d) Ta có: \(AH^4=\left(AH^2\right)^2=\left(BH.CH\right)^2=BH^2.CH^2\)
\(=BE.BA.CF.CA=BE.CF.\left(AB.AC\right)=BE.CF.AH.BC\)
\(\Rightarrow BC.BE.CF=AH^3\)
e) Ta có: \(AE.BE+AF.CF=EH^2+HF^2=EF^2=AH^2=BH.CH\)
f) Ta có: \(3AH^2+BE^2+CF^2=3AH^2+BH^2-EH^2+CH^2-HF^2\)
\(=3AH^2+BH^2+CH^2-\left(EH^2+HF^2\right)\)
\(=3AH^2+BH^2+CH^2-EF^2=3AH^2+BH^2+CH^2-AH^2\)
\(=BH^2+CH^2+2AH^2=BH^2+CH^2+2BH.CH\)
\(=\left(BH+CH\right)^2=BC^2\)

a) \(1+tan^2B=1+\dfrac{AC^2}{AB^2}=\dfrac{AB^2+AC^2}{AB^2}=\dfrac{BC^2}{AB^2}=\dfrac{1}{\left(\dfrac{AB}{BC}\right)^2}=\dfrac{1}{cos^2B}\)
b) Ta có: \(a.sinB.cosB=BC.\dfrac{AC}{BC}.\dfrac{AB}{BC}=\dfrac{AC.AB}{BC}=\dfrac{AH.BC}{BC}=AH\)
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=BC.\left(\dfrac{AB}{BC}\right)^2=BC.cos^2B\)
Tương tự \(\Rightarrow CH=BC.sin^2B\)

Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông đối với tam giác vuông $AHB$, đường cao $HE$:
$EA.EB=HE^2$
Tương tự: $FA.FC=HF^2$
$\Rightarrow EA.EB+FA.FC=HE^2+HF^2=EF^2(1)$ (định lý Pitago)
Mặt khác: Dễ thấy $HEAF$ là hình chữ nhật do có 3 góc $\widehat{E}=\widehat{A}=\widehat{F}=90^0$
$\Rightarrow EF=HA$
$\Rightarrow EF^2=HA^2(2)$
Áp dụng hệ thức lượng trong tam giác vuông $ABC$:
$AH^2=HB.HC(3)$
Từ $(1);(2); (3)\Rightarrow EA.EB+FA.FC=HB.HC$ (đpcm)

Áp dụng định lý pytago ta có :
`AC^2+AB^2=BC^2`
hay `16^2+12^2=BC^2`
`=>BC^2=400`
`=>BC=20(cm)`