a: BC vuông góc SA

BC vuôg góc AB

=>BC vuông góc (SAB)

b: BI vuông góc SA
BI vuông góc AC

=>BI vuông góc (SAC)

Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)

\(\Rightarrow BC=d\left(C;\left(SAB\right)\right)\)

\(\Rightarrow d\left(C;\left(SAB\right)\right)=2a\)

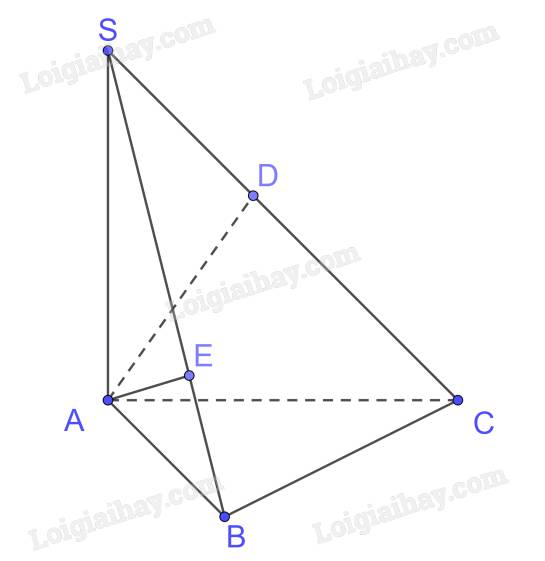
a) \(SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right),AB \bot BC \Rightarrow BC \bot \left( {SAB} \right),BC \subset \left( {SBC} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\)

b) +) Trong (SAC) kẻ \(AD \bot SC \Rightarrow d\left( {A,SC} \right) = AD\)

Xét tam giác ABC vuông tại B có

\(\sin \widehat {CAB} = \frac{{BC}}{{AC}} \Rightarrow AC = \frac{a}{{\sin {{30}^0}}} = 2a\)

Xét tam giác SAC vuông tại A có

\(\frac{1}{{A{D^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {2a} \right)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow AD = \frac{{2a\sqrt 3 }}{3}\)

Do đó \(d\left( {A,SC} \right) = \frac{{2a\sqrt 3 }}{3}\)

+) \(\left( {SAB} \right) \bot \left( {SBC} \right),\left( {SAB} \right) \cap \left( {SBC} \right) = SB\)

Trong (SAB) kẻ \(AE \bot SB\)

\( \Rightarrow AE \bot \left( {SBC} \right) \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AE\)

Xét tam giác ABC vuông tại B có

\(\tan \widehat {CAB} = \frac{{BC}}{{AB}} \Rightarrow AB = \frac{a}{{\tan {{30}^0}}} = a\sqrt 3 \)

Xét tam giác SAB vuông tại A có

\(\frac{1}{{A{E^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} = \frac{5}{{6{a^2}}} \Rightarrow AE = \frac{{a\sqrt {30} }}{5}\)

Vậy \(d\left( {A,\left( {SBC} \right)} \right) = \frac{{a\sqrt {30} }}{5}\)

Ta có: H là trung điểm SA, K là trung điểm AB

\(\Rightarrow\) HK là đường trung bình tam giác SAB

\(\Rightarrow HK||SB\)

Mà \(SB\perp\left(ABC\right)\Rightarrow HK\perp\left(ABC\right)\)

\(\Rightarrow HK\perp AB\) (1)

I là trung điểm BC, K là trung điểm AB \(\Rightarrow\) IK là đường trung bình tam giác ABC

\(\Rightarrow IK||AC\Rightarrow IK\perp AB\)  (2) (do \(AB\perp AC\) theo gt)

(1);(2) \(\Rightarrow AB\perp\left(IHK\right)\Rightarrow AB\perp IH\)

a. Ta có: \(\left\{{}\begin{matrix}AB\perp BC\\SA\perp BC\end{matrix}\right.\)\(\Rightarrow BC\perp\left(SAB\right)\)

b. Ta có: \(\left\{{}\begin{matrix}AH\perp SB\\AH\perp BC\:\left(BC\perp\left(SAB\right)\right)\end{matrix}\right.\)\(\Rightarrow AH\perp\left(SBC\right)\)

\(\Rightarrow AH\perp SC\)

Tự vẽ hình nhé:

a, Ta có: \(BC\perp AB\) (\(\Delta ABC\) vuông tại \(B\))

\(SA\perp BC\left(SA\perp\Delta ABC;BC\subset\left(ABC\right)\right)\)

\(AB\cap SA=\left\{A\right\}\)

\(AB,SA\subset\left(SAB\right)\)

\(\Rightarrow BC\perp\left(SAB\right)\)

b, Ta có \(BC\perp\left(SAB\right)\left(cmt\right)\)

mà \(SA\subset\left(SAB\right)\)

\(\Rightarrow BC\perp SA\)