cho hình vuông ABCD gọi E, K lần lượt là trung điểm của AB và CD. O là giao điểm của AK và DE kẻ \(DM\perp CE\)
a) chứng minh tứ giác ABKE là hình chữ nhật
b) chứng minh \(AK\perp DM\)
c) AK cắt BM tại N chứng minh tam giác ADM cân. tính góc ANB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QA
28 tháng 11 2023
a)ta có:
AB=DC mà AE=1/2 AB, KC= 1/2 DC
=>AE=KC
Xét tứ giác AECK, ta có:
AE//KC(AB//KC và AE thuộc AB và KC thuộc DC)
=>tứ giác AECK là hình bình hành.
b) chỗ DE vuông góc CE có đúng không vậy để mai mình làm tiếp
16 tháng 11 2021
a: Xét tứ giác AICK có
AI//CK
AI=CK
Do đó: AICK là hình bình hành
21 tháng 9 2021
a: Xét tứ giác DMBN có
BM//DN
BM=DN
Do đó: DMBN là hình bình hành
b: Xét ΔAKB có
M là trung điểm của AB
MH//BK
Do đó: H là trung điểm của AK
Xét ΔCHD có
N là trung điểm của CD
NK//DH
Do đó: K là trung điểm của HC
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
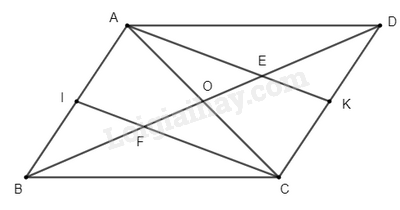
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AB\) // \(CD\), \(AD\) // \(BC\); \(AB = CD\); \(AD = BC\)
Mà \(IA = IB = \frac{{AB}}{2}\); \(KD = KC = \frac{{CD}}{2}\) (do \(I\),\(K\) là trung điểm)
Suy ra \(IA = IB = KD = KC\)
Xét tứ giác \(AKCI\) có:
\(AI = KC\) (cmt)
\(AI\) // \(KC\)
Suy ra \(AKCI\) là hình bình hành
Suy ra \(IC\) // \(AK\)
Hay \(IF\) // \(AE\)
Suy ra \(AEFI\) là hình thang
b) Vì \(ABCD\), \(AKCI\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\), \(BD\), \(KI\)
Suy ra \(OD = OB = \frac{1}{2}BD\) (1)
Xét tam giác \(ADC\) có hai trung tuyến \(AK\), \(DO\) cắt nhau tại \(E\)
Suy ra \(E\) là trọng tâm của tam giác
Suy ra \(ED = \frac{2}{3}DO\) (2)
Chứng minh tương tự ta có \(BF = \frac{2}{3}BO\) (3)
Từ (1), (2), (3) suy ra \(ED = BF = \frac{1}{3}BD\)
Suy ra \({\rm{EF}} = \frac{1}{3}BD\)
Vậy \(DE = EF = FB\)
25 tháng 11 2023
1: E là trung điểm của AB
=>\(EA=EB=\dfrac{AB}{2}\)(1)
K là trung điểm của CD
=>\(DK=KC=\dfrac{DC}{2}\)(2)
ABCD là hình vuông
=>AB=DC(3)
Từ (1),(2),(3) suy ra AE=EB=CK=KD
Xét tứ giác AECK có
AE//CK
AE=CK
Do đó: AECK là hình bình hành
2: Xét ΔFCD vuông tại C và ΔEBC vuông tại B có
FC=EB
CD=BC
Do đó: ΔFCD=ΔEBC
=>\(\widehat{FDC}=\widehat{ECB}\)
mà \(\widehat{FDC}+\widehat{DFC}=90^0\)(ΔDFC vuông tại C)
nên \(\widehat{ECB}+\widehat{DFC}=90^0\)
=>DF\(\perp\)CE tại M
3: AECK là hình bình hành
=>AK//CE
AK//CE
CE\(\perp\)DF
Do đó: AK\(\perp\)CE tại N
Xét ΔDMC có
K là trung điểm của DC
KN//MC
Do đó: N là trung điểm của DM
4: Xét ΔADM có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔADM cân tại A
=>AD=AM
mà AD=AB
nên AM=AB
a: Xét tứ giác ADKE có
AE//DK
AE=DK
góc EAD=90 độ
=>ADKE là hình chữ nhật
b: Xét tứ giác AECK có
AE//CK
AE=CK
=>AECK là hình bình hành
=>AK//EC
=>AK vuông góc DM