Cho đường tròn (O 3 cm) và dây MN =3√2
Tính diện tích hình quạt tròn OMN
Tính diện tích hình viên phân giới hạn MN, và cung nhỏ MN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc BOC=2*góc A=90 độ
=>OB^2+OC^2=BC^2
=>2*R^2=2^2=4
=>R=căn 2
\(S_{\left(O\right)}=R^2\cdot pi=2pi\left(cm^2\right)\)
b: \(S_{q\left(BOC\right)}=pi\cdot2\cdot\dfrac{90}{360}=\dfrac{1}{2}\cdot pi\left(cm^2\right)\)
\(S_{BOC}=\dfrac{1}{2}\cdot OB\cdot OC=\dfrac{1}{2}\cdot2=1\)
=>\(S_{viênphân}=\dfrac{1}{2}\cdot3.14-1=0.57\left(cm^2\right)\)

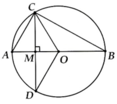
a, AC = 4cm => BC = 4 3 cm
=> R = 4cm => C = 8πcm, S = 16π c m 2
b, ∆AOC đều => A O C ^ = 60 0
=> C O D ^ = 120 0 => l C A D ⏜ = π . 4 . 120 180 = 8 π 3 cm
=> S = 8 π 3 . 4 2 = 16 π 3 c m 2
OM^2+ON^2=MN^2
OM=ON
=>ΔOMN vuông cân tại O
\(S_{q\left(OMN\right)}=\dfrac{pi\cdot3^2\cdot90}{360}=2.25pi\)
b: \(S_{OMN}=\dfrac{1}{2}\cdot OM\cdot ON=4.5\left(cm^2\right)\)
\(S_{VP\left(MN\right)}=2.25pi-4.5\)(cm2)