cho nửa đg tròn tâm O có đg kính AB=2R.Trên tia tới của tia AB lấy điểm M bất kỳ từ M. Vẽ đg thẳng ko đi qua O,đg thẳng này cắt nửa đg tròn O tại C và D(C nằm giữa M và D).Gọi I là giao điểm của AD và BC vẽ IE vuông góc vs AB

a)CM:ΔMAD đồng dạng ΔMCB.Từ đó suy ra MA.MD=MC.MD

b)CM:tg BDIE nt

c)CM:DI là tia phân giác của góc CDE

 Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh:

          1) Các tứ giác: ACMD; BCKM nội tiếp đường tròn.

          2) CK.CD = CA.CB

          3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh  B, K, N thẳng hàng

cho nửa đường tròn (o; ab)c là điểm nằm giữa o và a ,đường thẳng vuông góc với ab . tại c cắt nửa đường tròn tại i , k là điểm bất kỳ nằm trên đoạn thẳng ci (k khác c và i) , tia ak cắt nửa đường tròn (o) tại m, tia bm cắt tia ci tại d. chứng minh: a, các tứ giác acmd, bckm nội tiếp đường tròn. b, ck.cd = ca.cb. c, gọi n là giao điểm của ad và đường tròn (o) chứng minh b,k,n thẳng hàng

Giải hộ mình bài này nhé. Mình cần RẤT GẤP!!!!!!! : Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh: a) Tứ giác ACMD, BCKM nội tiếp đường tròn. b) CK.CD=CA.CB c) Gọi giao điểm của AD và nửa đường tròn (O) là N. Chứng minh B,K,N thẳng hàng. d) Tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định khi K di động trên đoạn thẳng CI.

Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng

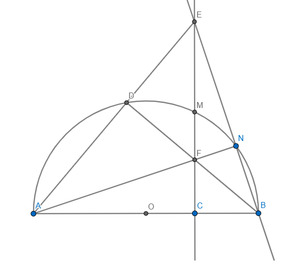
Cho nửa đường tròn (O) đường kính AB. Gọi C là điểm cố định thuộc đoạn thẳng OB (C khác O và B). Dựng đường thẳng d vuông góc với AB tại điểm C, cắt nửa đường tròn (O) tại điểm M. Trên cung nhỏ MB lấy điểm N bất kỳ (N  khác M và B), tia AN cắt đường thẳng d tại điểm F, tia BN cắt đường thẳng d tại điểm E. Đường thẳng AE cắt nửa đường tròn (O) tại điểm D (D khác A).

            a) Chứng minh tứ giác BCFN nội tiếp được một đường tròn.

            b) Chứng minh: AD.AE = AC.AB.

Cho nửa đường tròn (O) đường kính AB. Gọi C là điểm cố định thuộc đoạn thẳng OB (C khác O và B). Dựng đường thẳng d vuông góc với AB tại điểm C, cắt nửa đường tròn (O) tại điểm M. Trên cung nhỏ MB lấy điểm N bất kỳ (N  khác M và B), tia AN cắt đường thẳng d tại điểm F, tia BN cắt đường thẳng d tại điểm E. Đường thẳng AE cắt nửa đường tròn (O) tại điểm D (D khác A).

CM : góc EDN=góc DAB

Cho nửa đường tròn (O) đường kính AB. Gọi C là điểm cố định thuộc đoạn thẳng OB (C khác O và B). Dựng đường thẳng d vuông góc với AB tại điểm C, cắt nửa đường tròn (O) tại điểm M. Trên cung nhỏ MB lấy điểm N bất kỳ (N  khác M và B), tia AN cắt đường thẳng d tại điểm F, tia BN cắt đường thẳng d tại điểm E. Đường thẳng AE cắt nửa đường tròn (O) tại điểm D (D khác A).

CM : góc EDN=góc DAB