 Giups mình câu b ạ
Giups mình câu b ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



i: ĐKXĐ: \(\left[{}\begin{matrix}x\ge\sqrt{5}+1\\x\le-\sqrt{5}+1\end{matrix}\right.\)
l:ĐKXĐ: \(\left[{}\begin{matrix}x\ge3\\x\le-5\end{matrix}\right.\)
m: ĐKXĐ: \(\left[{}\begin{matrix}x\ge4\\x\le3\end{matrix}\right.\)
n: ĐKXĐ: \(x\in R\)


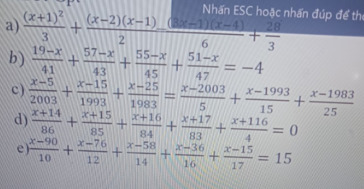
d: \(\Leftrightarrow\dfrac{x+14}{86}+1+\dfrac{x+15}{85}+1+\dfrac{x+16}{84}+1+\dfrac{x+17}{83}+1+\dfrac{x+116}{4}-4=0\)
=>x+100=0
hay x=-100
a: \(\Leftrightarrow2\left(x+1\right)^2+3\left(x^2-3x+2\right)=\left(3x-1\right)\left(x-4\right)+56\)
\(\Leftrightarrow2x^2+4x+2+3x^2-9x+6-\left(3x^2-13x+4\right)-56=0\)
\(\Leftrightarrow5x^2-5x-48-3x^2+13x-4=0\)
\(\Leftrightarrow2x^2+8x-52=0\)
\(\Leftrightarrow x^2+4x-13=0\)
\(\Leftrightarrow\left(x+2\right)^2=17\)
hay \(x\in\left\{-\sqrt{17}-2;\sqrt{17}-2\right\}\)


Pt hoành độ giao điểm:
\(x^2=-2\left(m-2\right)x-m^2+4m\Leftrightarrow x^2+2\left(m-2\right)x+m^2-4m=0\) (1)
\(\Delta'=\left(m-2\right)^2-\left(m^2-4m\right)=4>0;\forall m\Rightarrow\) (1) luôn có 2 nghiệm pb hay (d) luôn cắt (P) tại 2 điểm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2\left(m-2\right)\\x_1x_2=m^2-4m\end{matrix}\right.\)
Để biểu thức đề bài xác định \(\Rightarrow x_1x_2\ne0\Rightarrow\left[{}\begin{matrix}m\ne0\\m\ne4\end{matrix}\right.\)
Khi đó:
\(\dfrac{3}{x_1}+x_2=\dfrac{3}{x_2}+x_1\Leftrightarrow\left(3+x_1x_2\right)x_2=\left(3+x_1x_2\right)x_1\)
\(\Leftrightarrow\left(3+x_1x_2\right)\left(x_1-x_2\right)=0\)
\(\Leftrightarrow3+x_1x_2=0\) (do \(\Delta>0\) nên \(x_1-x_2\ne0\) với mọi m)
\(\Leftrightarrow3+m^2-4m=0\Rightarrow\left[{}\begin{matrix}m=1\\m=3\end{matrix}\right.\)







b: AF*AB=AE*AC
=>AF/AC=AE/AB
mà góc A chung
nên ΔAFE đồng dạng với ΔACB
=>góc AFE=góc ACB