cho hình chữ nhật ABCD kẻ AH vuông góc với BD (H thuộc BD). Trên đoạn DH lấy điểm E ,trên cạnh BC lấy điểm F sao cho DE.CB=DH.CF.Chứng minh rằng:
a) AB2=BD.BH
b) góc DAE= góc CAF
c) AE vuông góc với EF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\widehat{BCD}+\widehat{BCN}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{BCN}=180^0-\widehat{BCD}=180^0-90^0\)
\(\Leftrightarrow\widehat{BCN}=90^0\)
hay \(\widehat{MCN}=90^0\)
Xét tứ giác MCNF có
\(\widehat{MCN}=90^0\)(cmt)
\(\widehat{FMC}=90^0\)(FM⊥BC)
\(\widehat{FNC}=90^0\)(FN⊥DC)
Do đó: MCNF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: ABCD là hình chữ nhật(gt)
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường và bằng nhau(Định lí hình chữ nhật)
mà AC cắt BD tại O(gt)
nên O là trung điểm chung của AC và BD; AC=BD
Xét ΔACF có
O là trung điểm của AC(cmt)
E là trung điểm của AF(gt)
Do đó: OE là đường trung bình của ΔACF(Định nghĩa đường trung bình của tam giác)
⇒OE//CF và \(OE=\dfrac{CF}{2}\)(Định lí 2 về đường trung bình của tam giác)
hay CF//BD(đpcm)

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
=>BA=BE
=>B nằm trên đường trung trực của AE(2)
Ta có: ΔBAD=ΔBED
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại trung điểm I của AE
c: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Ta có: AH\(\perp\)BC
DE\(\perp\)BC
Do đó: AH//DE
d: Ta có: \(\widehat{EDC}+\widehat{ACB}=90^0\)(ΔEDC vuông tại E)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{EDC}=\widehat{ABC}\)
e: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAK=ΔDEC
=>DK=DC và AK=EC
Ta có: BK=BA+AK
BC=BE+EC
mà BA=BE và AK=EC
nên BK=BC
=>B nằm trên đường trung trực của KC(3)
Ta có: DK=DC
=>D nằm trên đường trung trực của KC(4)
Ta có: MK=MC
=>M nằm trên đường trung trực của CK(5)
Từ (3),(4),(5) suy ra B,D,M thẳng hàng
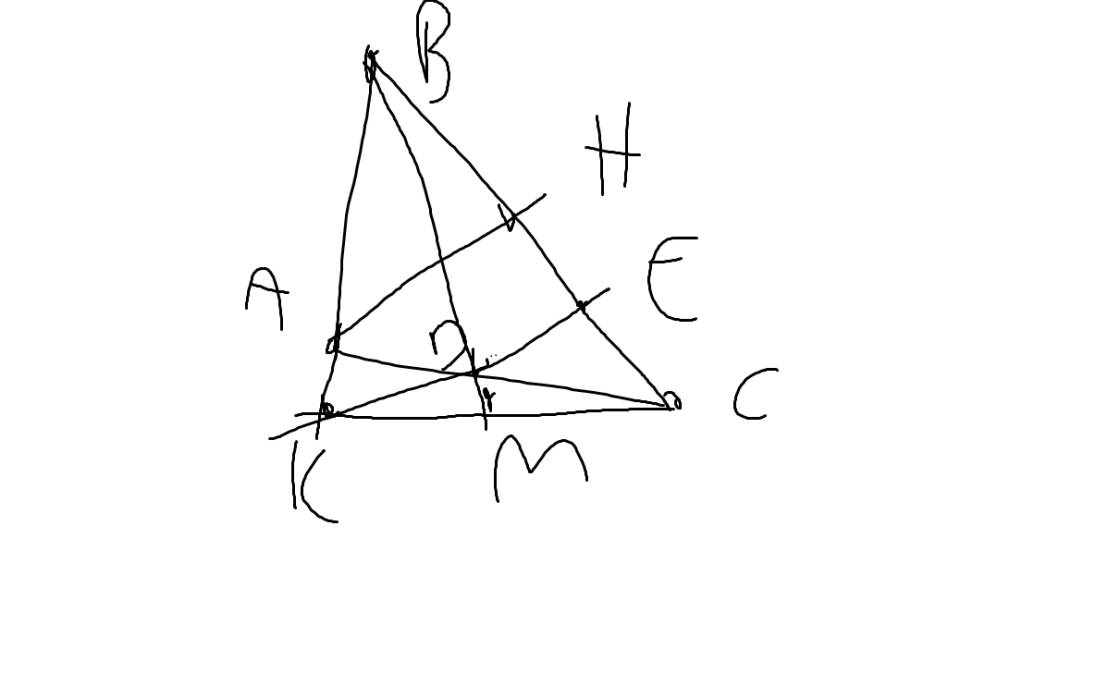

a: Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc B=góc C
=>ΔBHD=ΔCKE
=>HD=EK
b: Xét ΔAHD vuông tại H và ΔAKE vuông tại K có
AH=AK
HD=EK
=>ΔAHD=ΔAKE
=>AD=AE