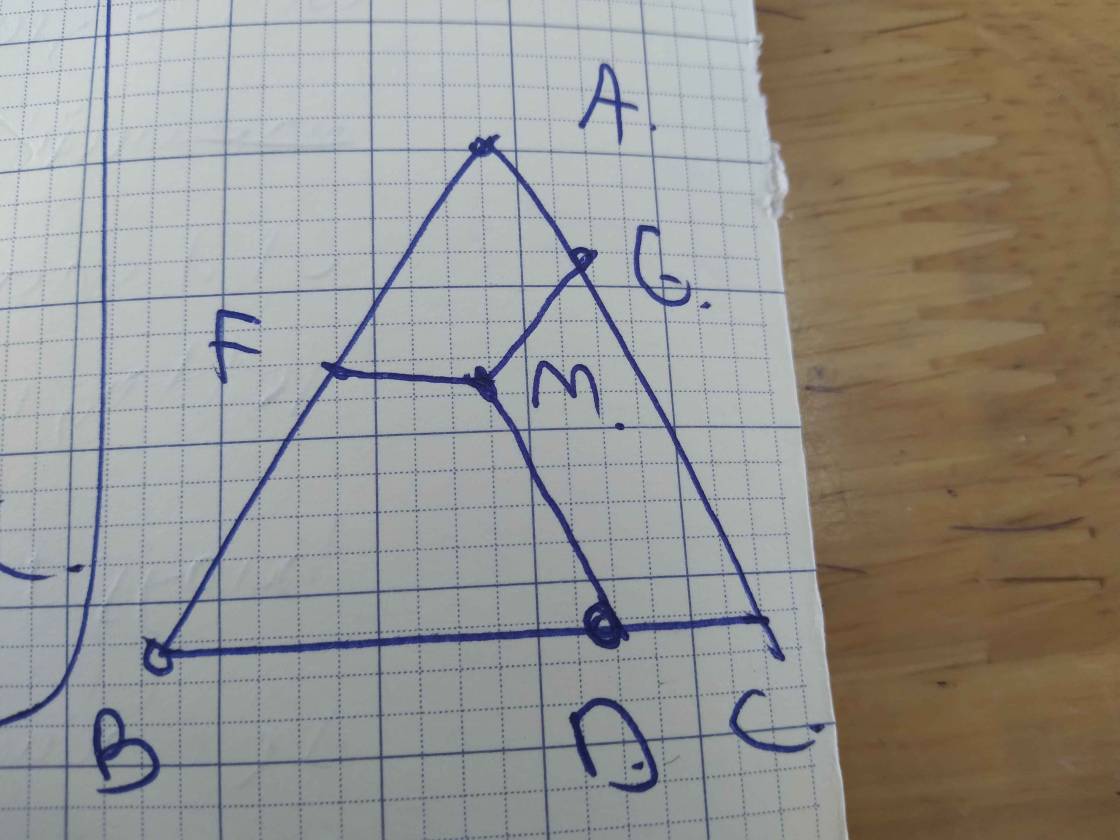
Cho tam giác đầu ABC. Điểm M nằm giữa B và C. Đường thẳng kẻ qua M và song song với AC cắt AB ở P, đường thẳng kẻ qua M và song song với AB cắt AC ở N.
a) Chứng minh tam giác BPM là tam giác đều
b) Gọi I là giao điểm của AM và PN, gọi O là trọng tâm của tam giác ABC. Chứng minh rằng tam giác OAN = tam giác OBP
c)Gọi H là 1 điểm trên đường thẳng BC sao cho HP = HN. Chứng minh rằng 3 điểm H,I,O thẳng hàng