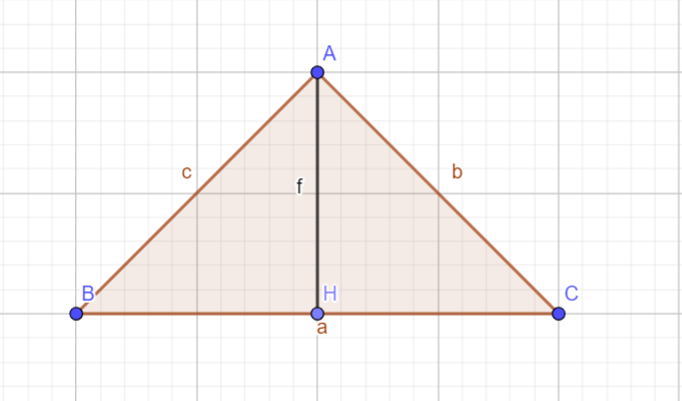
Cho hình tam giác ABC có góc A bằng 90 độ Kẻ AH vuông góc với BC . Biết rằng trong 1 tam giác tổng số đo 3 góc bằng 180 độ . Chứng minh rằng :
a ) Góc ABH bằng góc CAH
b) Góc AB bằng góc BAH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì \(\widehat{A}=90^o\rightarrow AB\perp AC\)
Mà \(HE\perp AC\)
-> AB song song với HE
b) Vì AB song song với HE (theo a)
=> \(\widehat{ABH}=\widehat{EHC}=50^o\)(2 góc đồng vị)
Ta có: \(\widehat{AHE}+\widehat{EHC}=\widehat{AHC}\)
\(\Rightarrow\widehat{AHE}+50^o=90^o\left(AH\perp BC\right)\)
\(\Rightarrow\widehat{AHE}=90^o-50^o=40^o\)
Vì AB song song với HE
=> \(\widehat{AHE}=\widehat{BAH}=40^o\)(2 góc so le trong)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC và \(\widehat{BAH}=\widehat{CAH}\)
b: Ta có: HB=HC
H nằm giữa B và C
Do đó: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=4\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-4^2=9\)
=>\(AH=\sqrt{9}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H

a) Xét tam giác AHB và AHC có:
AC = BC (gt)
\(\widehat{AHB}=\widehat{AHC}\) (AH vuông góc BC)
=> AHB = AHC (ch-gv)
=> HB = HC (cạnh tương ứng)
\(\widehat{BAH}=\widehat{CAH}\) (góc tương ứng)
b) Ta có HB = HC (cmt)
Mặt khác AH là cạnh góc vuông của tam giác vuông AHC
Áp dụng định lý Pitago ta có:
\(AC^2=AH^2+HC^2\\ =>10^2=AH^2+6^2\\ =>100=AH^2+36\)
\(=>AH^2=100-36=64\\ =>AH=\sqrt{64}=8\)

a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là tia phân giác của góc BAC
=>HB=HC và góc BAH=góc CAH
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: AD=AE và HD=HE
hay ΔHED cân tại H
trong tam giác, tổng số đo 3 góc=180 => trong tam giác vuông, 2 góc còn lại có tổng số đo=90
Xét tam giác ABC: góc A=90
=> góc ABC+góc ACB=90
tam giác AHC: góc H=90
=> góc CAH+ACB=90
=> góc ABH=góc CAH ( cùng + góc C=90)
b) tam giác AHB: góc H=90
=> góc BAH+góc B=90
mà ta có: B+ góc C=90
=> góc BAH=góc C