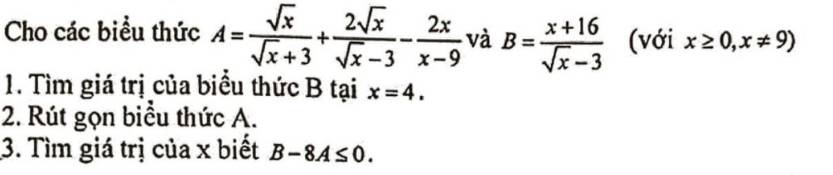
Làm giúp em câu c vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c. Dễ chứng minh 5 điểm A, N, F, H, E cùng thuộc đường tròn đường kính AH.
\(\Rightarrow HN\perp AN\left(1\right)\)
Vẽ đường kính AM của (O) \(\Rightarrow MN\perp AN\left(2\right)\)
Từ (1), (2) suy ra 3 điểm M, H, N thẳng hàng (3)
Dễ chứng minh BHCM là hình bình hành (BH // CM do cùng vuông góc với AC, tương tự 2 cạnh còn lại)
\(\Rightarrow\) 3 điểm H, I, M thẳng hàng (4)
Từ (3), (4) suy ra 3 điểm N, H, I thẳng hàng.

Bài 77:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{9}=\dfrac{y-x}{9-8}=5\)
Do đó: x=40; y=45


3.2:
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=m^2+m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1+x_2\right)^2=\left(2m+2\right)^2=4m^2+8m+4\\4x_1x_2=4m^2+4m\end{matrix}\right.\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4m+4=2\left(2m+2\right)=2\left(x_1+x_2\right)\)
\(\Rightarrow\left(x_1+x_2\right)^2-4x_1x_2-2\left(x_1+x_2\right)=4m^2+8m+4-4m^2-4m-4m-4=0\)
Vậy hệ thức liên hệ giữa \(x_1\) và \(x_2\) mà không phụ thuộc vào tham số m là \(\left(x_1+x_2\right)^2-4x_1x_2-2\left(x_1+x_2\right)\)
2: x1+x2=2m+2; x1x2=m^2+m
(x1+x2)^2-4x1x2
=4m^2+8m+4-4m^2-4m=4m+4
=>(x1+x2)^2-4x1x2-2(x1+x2)=4m+4-4m-4=0 ko phụ thuộc m


uses crt;
var a:array[1..100] of integer;
i,n,d,tong :integer;
begin
clrscr;
d:=0;
tong:=0;
readln(n);
for i:=1 to n do
readln(a[i]);
end;
for i:=1 to n do
if (a[i]>0) then begin
d:=d+1;
if d=1 then begin writeln('trong day co so nguyen duong '); write(' vi tri cua cac so duong ',i); end
else
begin
tong:=tong+a[i];
write(' ',i);
end;
end
else if ((i=n)and(d=0)) then write(' khong co so duong');
writeln;
writeln(' tong so luong so nguyen duong trong day so: ',d);
writeln(' ton cac so nguyen duong: ',tong);
readln;
end.

Lời giải:
a. TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(x)=|x|=|-x|=f(-x)$
$\Rightarrow $ hàm chẵn
b. TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=9; -f(1)=-9; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$ nên hàm không chẵn không lẻ.
c.
TXĐ: $\mathbb{R}$
Với $x\in\mathbb{R}$ thì $-x\in\mathbb{R}$
$f(-x)=(-x)^3+(-x)=-(x^3+x)=-f(x)$ nên hàm lẻ
d.
TXĐ: $\mathbb{R}$
Với $1\in\mathbb{R}$ thì $-1\in\mathbb{R}$
$f(1)=3; f(-1)=1$
$\Rightarrow f(1)\neq f(-1); -f(1)\neq f(-1)$
Do đó hàm không chẵn không lẻ.


Rút gọn được \(A=\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(B-8A\le0\Leftrightarrow\dfrac{x+16}{\sqrt{x}-3}-\dfrac{8\sqrt{x}}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\dfrac{x-8\sqrt{x}+16}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-4\right)^2}{\sqrt{x}-3}\le0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}-4=0\\\sqrt{x}-3< 0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=16\\x< 9\end{matrix}\right.\)
Kết hợp ĐKXD ta được: \(\left[{}\begin{matrix}x=16\\0\le x< 9\end{matrix}\right.\)