Cho đường tròn (O,R) dây cung MN (MN<2R) .Trên tia dối của tia MN lấy điểm A. từ A kẻ tiếp tuyến AAB<AC tới đường tròn O.
c) GỌi I là trung điểm của MN. Kẻ BI cắt dường tròn tại E. Cm EC//với AN.
(gợi ý:Nên Cm tứ giác OBAC nội tiếp và Cm AB2 =AC2 =AM.AN để cm câu c)

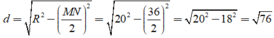
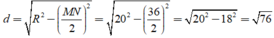
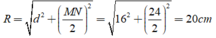
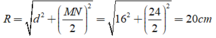
góc CEB=góc ACB(=1/2*sđ cung BC)
I là trung điểm của MN nên OI vuông góc MN
=>góc OIM=góc OIA=90 độ
góc OCA+góc OIA=180 độ
=>ACOI nội tiếp
mà ACOB nội tiếp
nên A,B,I,O,C cùng thuộc 1 đường tròn
=>góc AIB=góc ACB=góc EIN
=>góc CEB=góc EIN
=>MN//EC
=>AN//EC
Sao góc AIB=góc ACB mà lại suy ra góc CEB=góc EIN vậy ạ