Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC.
a) Chứng minh AH là phân giác của tam giác ABC
b) Gọi BK là phân giác của tam giác ABC (K thuộc AC), BK cắt AH tại I. Kẻ IM, IN vuông góc
với AB, AC (M, N thuộc AB, AC). Chứng minh IM = IN = IH.
c) Chứng minh IA là phân giác của góc MIN

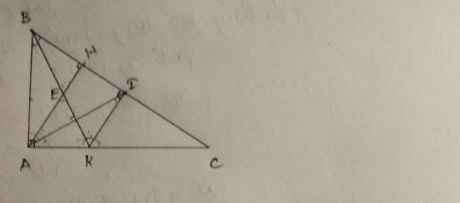
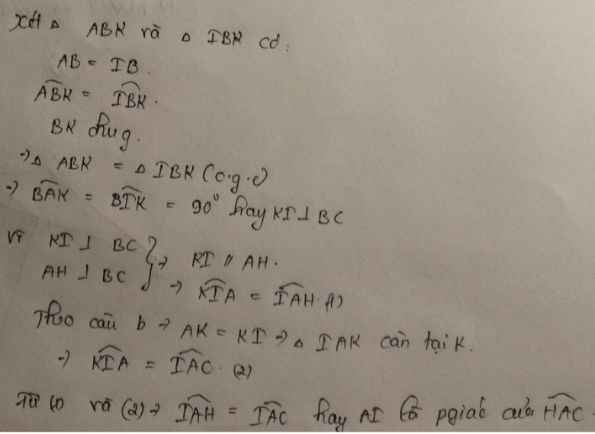
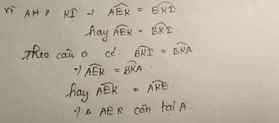
a: ΔBCA cân tạiA
mà AH là đường cao
nên AH là phân giác
b: Xet ΔBMI vuông tại M và ΔBHI vuông tại H có
BI chung
góc MBI=góc HBI
=>ΔBMI=ΔBHI
=>IM=IH
Xét ΔIMA vuông tại M và ΔINA vuông tại N có
AI chung
góc MAI=góc NAI
=>ΔIMA=ΔINA
=>IM=IN=IH
c: Xet ΔIMA vuông tại M và ΔINA vuông tại N có
AI chung
góc MAI=góc NAI
=>ΔIMA=ΔINA
=>góc MIA=góc NIA
=>IA là phân giác của góc MIN