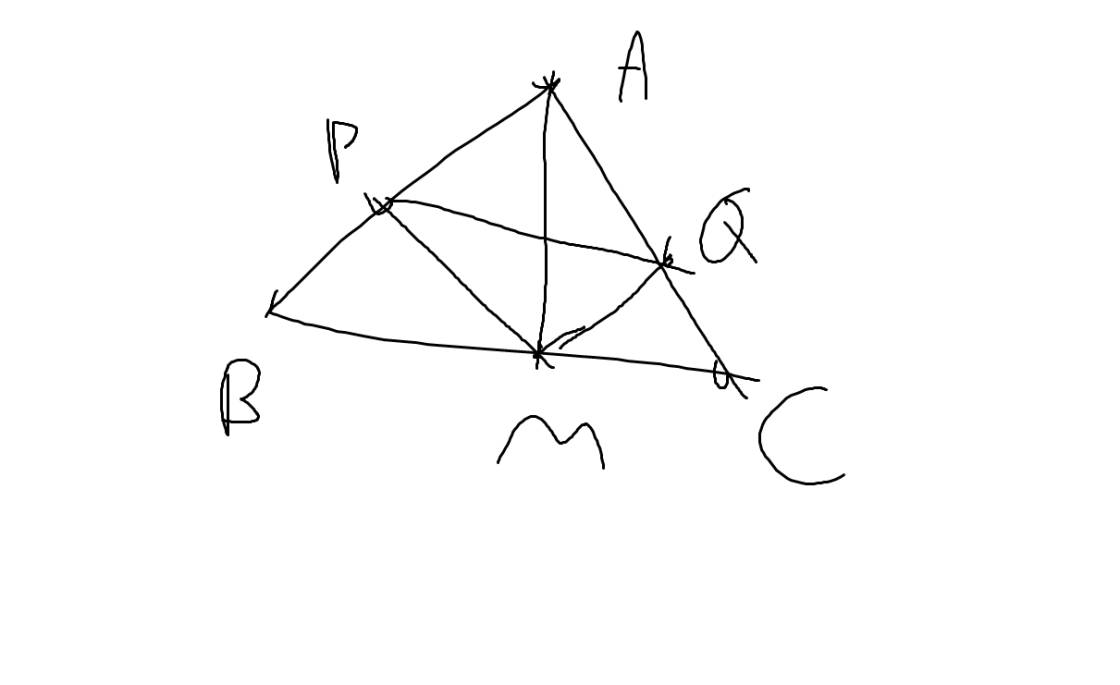
Cho tam giác đều ABC. Đường cao AH.M là một điểm thuộc cạnh BC(M khác A và B).từ M kẻ MP,MQ lần lượt vuông góc với AB,AC.
a/Chứng minh MP+MQ không đổi
b/Gọi O là trung điểm của AM.tứ giác POQH là hình gì
c/tìm vị trí của M trên BC để độ dài PQ là ngắn nhất