Đề khảo sát năng lực lớp 12, Sở GD-ĐT Hà Nội, mã đề 105:
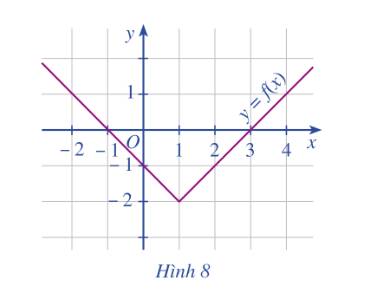
Câu 46. Cho hàm số \(f\left(x\right)=x^3-3x\). Số hình vuông có bốn đỉnh nằm trên đồ thị hàm số \(y=f\left(x\right)\) là?
A. 4 B. 2 C. 3 D. 1
Câu 47. Trong không gian Oxyz, cho điểm A(-2;6;0) và mặt phẳng (a): 3x + 4y + 89 = 0. Đường thẳng d thay đổi nằm trên mặt phẳng (Oxy) và luôn đi qua điểm A. Gọi H là hình chiếu vuông góc của M (4;-2;3) trên đường thẳng d. Khoảng cách nhỏ nhất từ H đến mặt phẳng (a) bằng?
A. 15 B. \(\dfrac{68}{5}\) C. 20 D. \(\dfrac{93}{5}\)


46.
Giả sử hình vuông ABCD tâm I, do I là tâm đối xứng hình vuông nên là tâm đối xứng đồ thị
\(\Rightarrow\) I là điểm uốn có tọa độ \(I\left(0;0\right)\) của hàm số
Do A đối xứng C, B đối xứng D qua I (đồng thời là gốc tọa độ) nên trong các cặp điểm AC và BD luôn có 2 điểm mang hoành độ dương và 2 điểm mang hoành độ âm, ko mất tính tổng quát, giả sử A và B mang hoành độ dương. Gọi \(A\left(a;a^3-3a\right)\) ; \(B\left(b;b^3-3b\right)\) với \(b>a>0\)
\(\Rightarrow C\left(-a;-a^3+3a\right)\) ; \(D\left(-b;-b^3+3b\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{CA}=\left(2a;2a^3-6a\right)\\\overrightarrow{DB}=\left(2b;2b^3-6b\right)\end{matrix}\right.\)
ABCD là hình vuông \(\Rightarrow\left\{{}\begin{matrix}AC=BD\\AC\perp BD\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a^2+\left(a^3-3a\right)^2=b^2+\left(b^3-3b\right)^2\\ab+\left(a^3-3a\right)\left(b^3-3b\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2+a^2\left(a^2-3\right)^2=b^2+b^2\left(b^2-3\right)^2\\1+\left(a^2-3\right)\left(b^2-3\right)=0\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}a^2-3=x>-3\\b^2-3=y>-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x+3+x^2\left(x+3\right)=y+3+y^2\left(y+3\right)\\xy=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)\left(x^2+xy+y^2+3x+3y+1\right)=0\\xy=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x+y\right)^2+3\left(x+y\right)+2=0\\xy=-1\end{matrix}\right.\) (do \(b>a>0\Rightarrow x\ne y\))
\(\Rightarrow\left[{}\begin{matrix}x+y=-1;xy=-1\\x+y=-2;xy=-1\end{matrix}\right.\)
Sử dụng Viet đảo ta được
\(\left(x;y\right)=\left(\dfrac{-1-\sqrt{5}}{2};\dfrac{-1+\sqrt{5}}{2}\right);\left(\dfrac{-1+\sqrt{5}}{2};\dfrac{-1-\sqrt{5}}{2}\right);\left(-1-\sqrt{2};-1+\sqrt{2}\right);\left(-1+\sqrt{2};-1-\sqrt{2}\right)\)
Do \(y>x\) nên chỉ có 2 cặp thỏa mãn. Mỗi giá trị x; y cho đúng 1 giá trị a; b dương tương ứng, nên có 2 cặp A; B thỏa mãn \(\Rightarrow\) có 2 hình vuông thỏa mãn (thực ra có thể tìm chính xác tọa độ A; B nhưng nó hơi xấu, ví dụ ứng với \(x=\dfrac{-1-\sqrt{5}}{2}\Rightarrow a^2=x+3=\dfrac{5-\sqrt{5}}{2}\Rightarrow a=\sqrt{\dfrac{5-\sqrt{5}}{2}}\) ko rút gọn được
47.
- Nhận xét quan trọng: hai mặt phẳng (a) và Oxy vuông góc (thấy ngay bằng dấu hiệu cả hai đều "khuyết z")
Từ nhận xét trên, ta thấy khoảng cách từ điểm H thuộc Oxy tới (a) chính là khoảng cách từ H tới d, với d là giao tuyến của (a) và mp Oxy.
Gọi K là hình chiếu vuông góc của M xuống Oxy \(\Rightarrow MK\perp Oxy\) với \(K\left(4;-2;0\right)\)
\(\Rightarrow MK\perp d\) ; mà \(d\perp MH\) theo giả thiết \(\Rightarrow d\perp\left(MHK\right)\)
\(\Rightarrow d\perp KH\) hay tam giác AHK vuông tại H
\(\Rightarrow\) Quỹ tích H là đường tròn đường kính AK thuộc mặt phẳng Oxy
Bây giở ta có 1 bài toán hình học phẳng đơn giản : cho 1 đường thằng cố định nằm ngoài đường tròn (O), tìm điểm M thuộc (O) sao cho khoảng cách từ M tới d đạt min. Lời giải đơn giản là qua tâm O đường tròn vẽ đường thẳng d' vuông góc d, d' cắt (O) tại A (với A nằm giữa O và d), khi đó khoảng cách từ A tới d sẽ ngắn nhất.
Trong bài toán này, để khỏi cần tính toán nhiều thì ta tính nhanh khoảng cách nhỏ nhất như sau:
Gọi I là trung điểm AK \(\Rightarrow I\left(1;2;0\right)\)
\(\Rightarrow d\left(H;\left(\alpha\right)\right)_{min}=d\left(I;\left(\alpha\right)\right)-\dfrac{AK}{2}\) (có biết tại sao có biểu thức này không?) \(=15\)