Đáp án A

Số phần tử của không gian mẫu  n Ω = C 9 3 = 84

Gọi A là biến cố sao cho ba quyển lấy ra có

ít nhất một quyển sách Toán.  ⇒ n A ¯ = C 5 3 = 10

⇒ A ¯ là biến cố sao cho ba quyển lấy ra không

 có sách Toán ⇒ n A ¯ = C 5 3 = 10 .

⇒ P A = 1 − P A ¯ = 1 − 10 84 = 37 42

Chọn D.

Lấy ngẫu nhiên 3 quyển sách có:  cách.

Gọi A là biến cố: 3 quyển được lấy ra có ít nhất một quyển toán.

Suy ra A ¯  là biến cố: lấy 3 quyển sách và không có quyển nào là quyển toán.

Khi đó

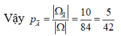
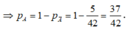
Đáp án C

Phương pháp giải: Sử dụng biến cố đối và các quy tắc đếm cơ bản.

Lời giải:

Chọn 3 quyển sách trong 15 quyển sách có  cách => n(Ω) = 455

Gọi X là biến cố 3 quyển sách được lấy ra có ít nhất một quyển sách là toán.

Và X là biến cố 3 quyển sách được lấy ra không có quyển sách toán. Khi đó, ta xét các trường hợp sau:

TH1. Lấy được 2 quyển lý, 1 quyển hóa => có  cách

TH2. Lấy được 1 quyển lý, 2 quyển hóa => có cách

TH3. Lấy được 3 quyển lý, 0 quyển hóa => có  cách

TH4. Lấy được 0 quyển lý, 3 quyển hóa => có  cách

Suy ra số phần tử của biến cố  X là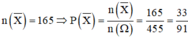 

Vậy xác suất cần tính là 

Đáp án C

Phương pháp giải: Sử dụng biến cố đối và các quy tắc đếm cơ bản.

Lời giải:

Chọn 3 quyển sách trong 15 quyển sách có C 15 3   =   455  cách  ⇒ n ( Ω )   =   455

Gọi X là biến cố 3 quyển sách được lấy ra có ít nhất một quyển sách là toán.

Và X  là biến cố 3 quyển sách được lấy ra không có quyển sách toán. Khi đó, ta xét các trường hợp sau:

TH1. Lấy được 2 quyển lý, 1 quyển hóa => có  C 5 2 . C 6 1   =   60  cách

TH2. Lấy được 1 quyển lý, 2 quyển hóa => có C 5 1 . C 6 2   =   75  cách

TH3. Lấy được 3 quyển lý, 0 quyển hóa => có C 5 3 . C 6 0 = 10 cách

TH4. Lấy được 0 quyển lý, 3 quyển hóa => có C 5 0 . C 6 3   =   20 cách

Suy ra số phần tử của biến cố  X là

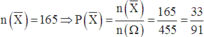
Vậy xác suất cần tính là

Đáp án D.

Đáp án D

Chọn đáp án C.

Số kết quả có thể khi chọn bất kì 3 quyển sách trong 9 quyển sách là C 9 3 = 84 .

Gọi A là biến có “Lấy được ít nhất 1 sách toán trong 3 quyển sách.”

A  là biến cố “Không lấy được sách toán trong 3 quyển sách.”

Ta có xác suất để xảy ra A là P A = 1 - P A = 1 - C 5 3 84 = 37 42 .

Đáp án C

Lấy ngẫu nhiên 3 cuốn sách có: C 9 3 = 84  cách

Gọi A là biến cố: Lấy 3 cuốn sách và không có cuốn nào là cuốn toán

Suy ra A ¯  là biến cố: 3 quyển được lấy ra có ít nhất một quyển là toán

Khi đó Ω A = C 5 3 = 10 .

Vậy p A = Ω A Ω = 10 84 = 5 42 ⇒ p A ¯ = 1 − p A = 37 42