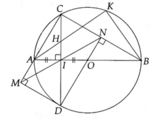
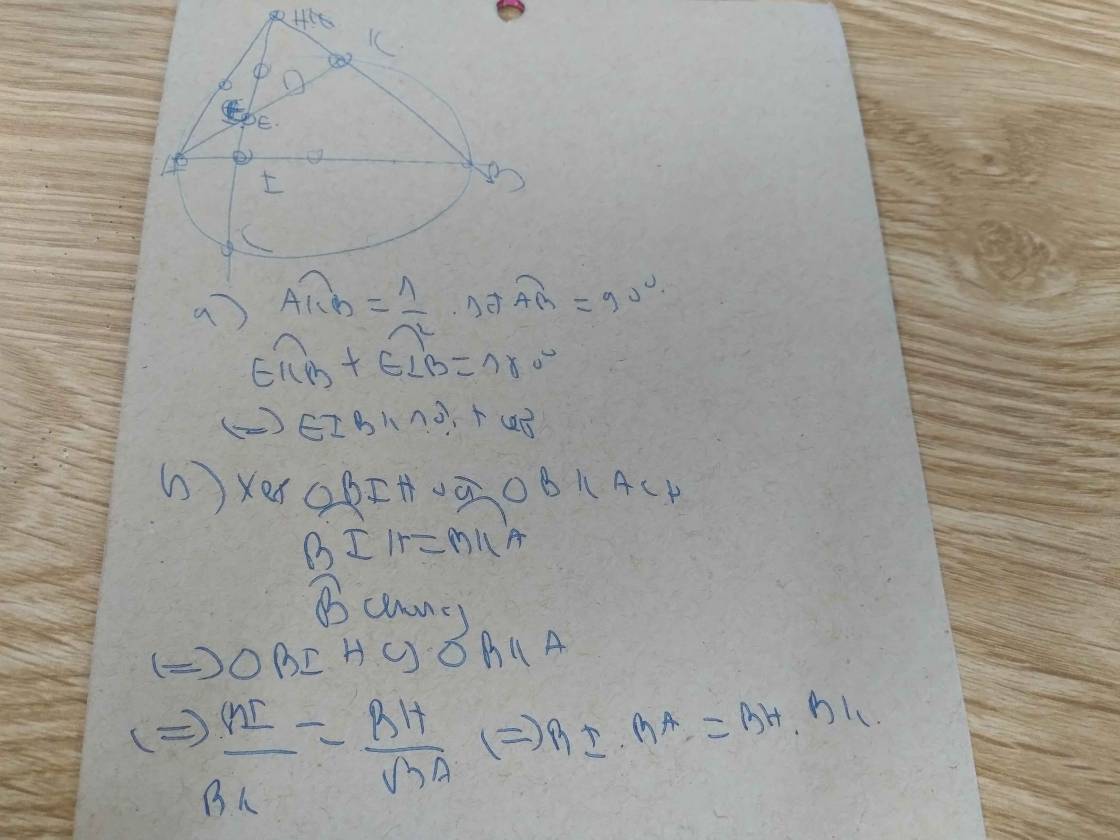Cho đường tròn (o) đường kính MN, dây CD vuông góc vớii Mn tại H. Trên CH lấy I, MI cắt đường tròn tại A. 

a) Chứng minh: tứ giác AIHN nội tiếp đường tròn

b) chứng minh: góc MCD = góc MAC

c) Chứng minh : MC\(^2\) = MI.MA

d) Gọi P là giao điểm của MA và CN

Gọi Q là giao điểm của AD và MN

chứng minh: P là tâm đường tròn nội tiếp tam giác ACQ

1. cho đường tròn (O) đường kính AB và dây CD vuông góc với AB tại F. trên cung BC lấy điểm M. nối A với M cắt CD tại E

a. chứng minh AM là phân gics của góc CMD

b. chứng minh tứ giác EFBM nội tiếp

c. chứng minh AC^2=AE.AM

2. cho đường tròn (O), dây MN và một điểm C ở ngoài đường tròn và nằm trên tia NM. từ một điểm chính giữa P của cung lớn MN kẻ đường kính PQ của đường tròn cắt dây MN tại D. tia CP cắt đường tròn (O) tại điểm thứ hai I. các dây MN và QI cắt nhau tại K

a. chứng minh rằng tứ giác PDKI nội tiếp

b. chứng minh CI.CP=CK.CD

có thể giúp tôi được không ạ?^^

Cho đường tròn tâm (o) đường kính AB, vẽ dây CD vuông góc với AB tại I ( I nằm giữa AK và B). Trên tia CD lấy điểm H nằm ngoài đường tròn ,HB cắt đường tròn tại K ( K khác B) A cắt CD tại E. a chứng minh tứ giác BKEI nội tiếp b chứng minh AB*BI = HB* BK c cho biết AB= 8 cm, AK = 7 cm.tính diện tích hình quạt tròn BOK ứng với cung nhỏ BK của đường tròn (O) ( kết quả làm tròn đến chữ số thập phân thứ nhất

Cho đường tròn tâm O đường kính AB. Dây cung MN vuông góc với AB tại I( I nằm giữa A và O). Trên tia NM lấy điểm K nằm ngoài đường tròn ( M nằm giữa N và K), AK cắt đường tròn tại C, CB cắt MN tại D. Chứng minh rằng:

a/ Tứ giác ACDI nội tiếp đường tròn. Xác định đường kính và tâm của đường tròn đó. 

b/ AB.DI = AC.BD

c/ AD cắt đường tròn tại E. Từ điểm C kẻ đường thẳng vuông góc với AE cắt EI tại F. Chứng minh ECF tam giác cân.

Cho đường tròn (O) đường kính AB, gọi I là trung điểm của OA, dây CD vuông góc với AB tại I.  Lấy K tùy ý trên cung BC nhỏ, AK cắt CD tại H

a, Chứng minh tứ giác BIHK là tứ giác nội tiếp

b, Chứng minh AHAK có giá trị không phụ thuộc vị trí điểm K

c, Kẻ DN ^ CB, DM ^ AC. Chứng minh các đường thẳng MN, AB, CD đồng quy

Cho đường tròn tâm O đường kính AB trên đường tròn lấy điểm D khác A và B . Trên đường kính AB lấy điểm C , kẻ CH vuông góc với AD tại H. Đường phân giác trong của góc DAB cắt đường tròn tại E và cắt CH tại F. đường thẳng DF cắt đường tròn tại N . chứng minh rằng 

a, góc ANF = góc ACF

b, Tứ giác AFCN nội tiếp đtròn

c, 3 điểm C,N,E thẳng hàng

( giúp mk với nhanh nha . mơn mn )

Cho đường tròn (O) có hai đường kính AB, CD không vuông góc với nhau.

a) Chứng minh: tứ giác ACBD là hình chữ nhật.

b) Tiếp tuyến tại A của đường tròn (O) cắt các đường thẳng BC, BD lần lượt tại E, F. Chứng minh: tứ giác ECDF nội tiếp.

c) Từ C và D vẽ các tiếp tuyến với đường tròn (O) cắt EF theo thứ tự tại M và N. Chứng minh: MN=12EF.

d) Gọi I là chân đường vuông góc hạ từ M xuống BN; H là giao điểm của AB và MI. Chứng minh: HA = HO.