Người thợ phải làm 300 sản phẩm trong 1 thời gian quy định.Nhờ tăng năng suất lao động nên mỗi ngày người đó làm thêm được 5 sản phẩm do với kế hoạch. Vì vậy người đó hoàn thành sớm hơn 3 ngày so với quy định. Tính số sản phẩm mà người thợ đó làm trong 1 ngày theo kế hoạch
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


| KLCV | Năng suất | Thời gian | |
| Kế hoạch | 1000 | x | \(\dfrac{1000}{x}\) |
| Thực tế | 1000+80=1080 | x+10 | \(\dfrac{1080}{x+10}\) |
Pt: \(\dfrac{1000}{x}-\dfrac{1080}{x+10}=2\)
Gọi số sản phẩm đội dự định làm mỗi ngày là x \(\left(x\in N,x< 100\right)\)( sản phẩm )
Theo kế hoạch
Thời gian hoàn thành là:\(\dfrac{1000}{x}\left(ngày\right)\)
Thực tế.
Mỗi ngày tổ làm được x+10 ( sản phẩm).
Thời gian hoàn thành : \(\dfrac{1080}{x+10}\)( ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
\(\dfrac{1000}{x}-\dfrac{1080}{x+10}=2\)
\(\Leftrightarrow\dfrac{500}{x}-\dfrac{540}{x+10}=1\) ( quy đồng đơn giản hơn để dễ làm )
\(\Leftrightarrow\dfrac{500.\left(x+10\right)-540x}{x\left(x+10\right)}=\dfrac{x\left(x+10\right)}{x\left(x+10\right)}\)
\(\Leftrightarrow500x+5000-540x=x^2+10x\) (quy đồng bỏ mẫu )
\(\Leftrightarrow x^2+50x-5000=0\)
\(\Leftrightarrow\) pt có 2 nghiệm phân biệt
th1 : x=-100 ( vô lí)
th2 x= 50 ( nhận )
Vậy...
Gọi \(x\) (ngày) là số ngày hoàn thành theo kế hoạch (\(x\) > 2)
Số sản phẩm mỗi ngày theo kế hoạch: \(\dfrac{1000}{x}\) (sản phẩm)
Số sản phẩm mỗi ngày thực làm: \(\dfrac{1000}{x}+10\)
Số ngày thực làm: \(x-2\) (ngày)
Theo đề bài ta có phương trình:
\(\left(\dfrac{1000}{x}+10\right).\left(x-2\right)=1080\)
\(\Leftrightarrow1000-\dfrac{2000}{x}+10x-20=1080\)
\(\Leftrightarrow10x^2+980x-1080x-2000=0\)
\(\Leftrightarrow10x^2-100x-2000=0\)
\(\Leftrightarrow x^2-10x-200=0\)
\(\Leftrightarrow x^2-20x+10x-200=0\)
\(\Leftrightarrow\left(x^2-20x\right)+\left(10x-200\right)=0\)
\(\Leftrightarrow x\left(x-20\right)+10\left(x-20\right)=0\)
\(\Leftrightarrow\left(x-20\right)\left(x+10\right)=0\)
\(\Leftrightarrow x-20=0;x+10=0\)
*) \(x-20=0\)
\(\Leftrightarrow x=20\) (nhận)
*) \(x+10=0\)
\(x=-10\) (loại)
Vậy số sản phẩm theo kế hoạch đội đó phải làm trong một ngày là: \(\dfrac{1000}{20}=50\) (sản phẩm)

Gọi số sản phẩm đội dự định làm mỗi ngày là x (x ∈ ℕ * , x < 84) (sản phẩm)
*) Theo kế hoạch, thời gian hoàn thành là 1000/x (ngày)
*) Thực tế, mỗi ngày làm được x + 10 (sản phẩm)
Thời gian hoàn thành 1000/(x+10) (ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
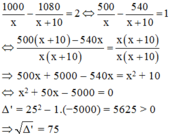
Phương trình có hai nghiệm phân biệt: x 1 = − 25 – 75 = −100 (loại)
và x 2 = −25 + 75 = 50 (tmđk)
Vậy theo kế hoạch, mỗi ngày tổ dự định làm 50 sản phẩm
Đáp án: C

https://h.vn/hoi-dap/tim-kiem?q=m%E1%BB%99t+t%E1%BB%95+c%C3%B4ng+nh%C3%A2n+theo+k%E1%BA%BF+ho%E1%BA%A1ch+ph%E1%BA%A3i+l%C3%A0m+120+s%E1%BA%A3n+ph%E1%BA%A9m+trong+m%E1%BB%99t+th%E1%BB%9Di+gian+nh%E1%BA%A5t+%C4%91%E1%BB%8Bnh+nh%C6%B0ng+khi+th%E1%BB%B1c+hi%E1%BB%87n+n%C4%83ng+su%E1%BA%A5t+c%E1%BB%A7a+t%E1%BB%95+%C4%91%C3%A3+v%C6%B0%E1%BB%A3t+n%C4%83ng+su%E1%BA%A5t+d%E1%BB%B1+%C4%91%E1%BB%8Bnh+l%C3%A0+10+s%E1%BA%A3n+ph%E1%BA%A9m+.+do+%C4%91%C3%B3+t%E1%BB%95+%C4%91%C3%A3+ho%C3%A0n+th%C3%A0nh+c%C3%B4ng+vi%E1%BB%87c+s%E1%BB%9Bm+h%C6%A1n+d%E1%BB%B1+%C4%91%E1%BB%8Bnh+m%E1%BB%99t+ng%C3%A0y+t%C3%ADnh+xem+th%E1%BB%B1c+t%E1%BA%BF+m%E1%BB%97i+ng%C3%A0y+t%E1%BB%95+%C4%91%C3%A3+l%C3%A0m+%C4%91%C6%B0%E1%BB%A3c+bao+nhi%C3%AAu+s%E1%BA%A3n+ph%E1%BA%A9m&id=230647

Gọi số sản phẩn dự kiến làm mỗi ngày là x>3 sản phẩm và thời gian dự định làm là y>2 ngày
\(\Rightarrow\) Số sản phẩm dự định làm là \(xy\) sản phẩm
Do tăng năng suất mỗi ngày 5 sản phẩm thì thời gian hoàn thành sớm hơn 2 ngày nên:
\(\left(x+5\right)\left(y-2\right)=xy\Rightarrow-2x+5y-10=0\)
Do giảm năng suất 3 sản phẩm mỗi ngày thì thời gian hoàn thành muộn 2 ngày nên:
\(\left(x-3\right)\left(y+2\right)=xy\Rightarrow2x-3y-6=0\)
Ta được hệ: \(\left\{{}\begin{matrix}-2x+5y-10=0\\2x-3y-6=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=15\\y=8\end{matrix}\right.\)
Công nhân đó được giao làm: \(15.8=120\) sản phẩm

Gọi x là số sản phẩm mỗi giờ mà người công nhân phải hoàn thành theo kế hoạch
(x ∈ ℕ * , x < 84)
Số sản phẩm mỗi giờ mà người công nhân phải hoàn thành theo thực tế: x + 2
Thời gian mà công nhân hoàn thành theo kế hoạch: 84/x (h)
Thời gian mà công nhân hoàn thành theo thực tế: 84/(x+2) (h)
Người công nhân đó hoàn thành công việc sớm hơn dự định 1 giờ nên ta có phương trình:
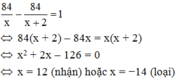
Vậy theo kế hoạch mỗi giờ người công nhân phải làm 12 sản phẩm
Đáp án: B

Gọi năng suất dự định là x (0 < x < 20, sản phẩm/giờ)
Sản phẩm làm được sau 2 giờ là: 2x (sản phẩm)
Số sản phẩm còn lại là 120 – 2x (sản phẩm)
Năng suất sau khi cải tiến là x + 3 (sản phẩm/giờ)
Thời gian làm số sản phẩm còn lại là: 120 - 2 x x + 3 (giờ)
Do sau khi cải tiến người đó hoàn thành kế hoạch sớm hơn dự định 1 giờ 36 phút
Đổi 1 giờ 36 phút bằng 1,6 giờ
Theo bài ra ta có phương trình:
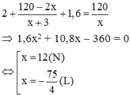
Vậy năng suất dự định của công nhân đó là 12 sản phẩm/giờ
Đáp án C
Lời giải:
Giả sử năng suất ban đầu là $a$ sản phẩm/ ngày.
Số ngày dự định: $\frac{300}{a}$ (ngày)
Năng suất sau khi tăng: $a+5$ (sản phẩm/ ngày)
Số ngày hoàn thành sản phẩm: $\frac{300}{a+5}$ (ngày)
Theo bài ra: $\frac{300}{a}-\frac{300}{a+5}=3$
Giải pt trên, với điều kiện $a>0$ suy ra $a=20$
Vậy theo kế hoạch thì người thợ đó làm 20sp/ ngày
Gọi số sản phẩm phải làm trong 1 ngày là x
Theo đề, ta có: \(\dfrac{300}{x}-\dfrac{300}{x+5}=3\)
=>100/x-100/x+5=1
=>(100x+500-100x)/(x^2+5x)=1
=>x^2+5x-500=0
=>(x+25)(x-20)=0
=>x=20