27,16:25=679/625=1 dư 54

bạn phải trả lời trên 3 dòng

phải đc ng khác tích

và ng tích phải có số điểm từ 10 SP trở lên

HT

Cách để tăng điểm hỏi đáp SP:

- Phải trả lời các câu hỏi

- Khi trả lời các câu hỏi phải trả lời trên 4 dòng

- Được người trên 10SP hoặc 11SP k 'Đúng'

- Mỗi lần người đó k 'Đúng' thì bạn sẽ tăng lên 1SP

a)2 + 5 + 11 + ... + 47+ 95
Tính chất : 5 = 2.2 + 1
11 = 5.2 + 1
Vậy các số của dãy là: 2 + 5 + 7 + 11 + 23 + 47 + 95
= (2 + 5 + 7) + (5 + 95) + (23 + 47)
= 14 + 100 + 70
= 184

2^x+2 - 2^x = 96

2^x . 2² - 2^x . 1 = 96

2^x . ( 2² - 1 ) = 96

2^x . 3 = 96

2^x = 32

2^x = 2⁵

=> x = 5

hok tốt

\(2^{x+2}-2^x=96\)

\(\Rightarrow2^x.\left(2^2-1\right)=96\)

\(\Rightarrow2^x.3=96\)

\(\Rightarrow2^x=96:3=32=2^5\)

\(\Rightarrow x=5\)

376 x 29 + 70 x 376 + 376

= 376 x 29 + 70 x 376 + 376 x 1

= 376 x (29 + 70 + 1)

= 376 x 100

= 37600

Sửa đề:

376 × 29  + 70 × 376 + 376

= 376 × (29 + 70 + 1)

= 376 × 100

= 37600

Bài III.2b.

Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)

hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)

\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có : 

\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)

\(=m^2+2m+1-4m-16\)

\(=m^2-2m-15>0\).

\(\Rightarrow m< -3\) hoặc \(m>5\).

Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)

\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)

\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)

Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).

Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)

Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)

\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).

Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).

Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt : 

\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)

Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).

Vậy : Không có giá trị m thỏa mãn đề bài.

Bài IV.b.

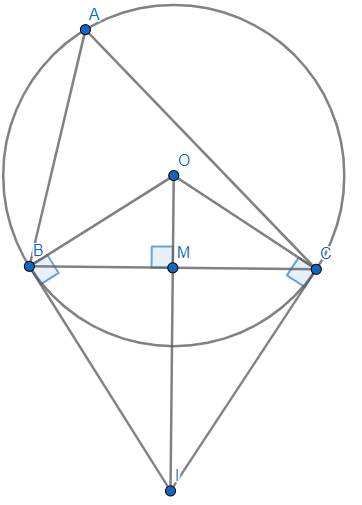
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).

Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).

Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).

Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).

Lại có : \(BC=MB+MC=2MB\)

\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)

Tính diện tích hình quạt tròn

Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).

\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)

`7,`

`a, B+A=4x-2x^2+3`

`-> B=(4x-2x^2+3)-A`

`-> B=(4x-2x^2+3)-(x^2-2x+1)`

`B=4x-2x^2+3-x^2+2x-1`

`B=(-2x^2-x^2)+(4x+2x)+(3-1)`

`B=-3x^2+6x+2`

`b, C-A=-x+7`

`-> C=(-x+7)+A`

`-> C=(-x+7)+(x^2-2x+1)`

`-> C=-x+7+x^2-2x+1`

`C=x^2+(-x-2x)+(7+1)`

`C=x^2-3x+8`

`c,`

`A-D=x^2-2`

`-> D= A- (x^2-2)`

`-> D=(x^2-2x+1)-(x^2-2)`

`D=x^2-2x+1-x^2+2`

`D=(x^2-x^2)-2x+(1+2)`

`D=-2x+3`

`6,`

`a,`

`P+Q=4x-2x^2+3`

`-> Q=(4x-2x^2+3)-P`

`-> Q=(4x-2x^2+3)-(3x^2+x-1)`

`Q=4x-2x^2+3-3x^2-x+1`

`Q=(-2x^2-3x^2)+(4x-x)+(3+1)`

`Q=x^2+3x+4`

`b,`

`x^2-5x+2-P=H`

`-> H= (x^2-5x+2)-(3x^2+x-1)`

`H=x^2-5x+2-3x^2-x+1`

`H=(x^2-3x^2)+(-5x-x)+(2+1)`

`H=-4x^2-6x+3`

`c,`

`P-R=5x^2-3x-4`

`-> R= P- (5x^2-3x-4)`

`-> R=(3x^2+x-1)-(5x^2-3x-4)`

`R=3x^2+x-1-5x^2+3x+4`

`R=(3x^2-5x^2)+(x+3x)+(-1+4)`

`R=-2x^2+4x+3`

chúc mừng :))

Chúc mừng mọi người!!!!!!!!!!!!!!!!!!!!!!