Nhờ quý thầy cô giảng giúp bài toán này cho bé. Mẹ cám ơn ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với p = 2 => 2p + p2 = 8 (loại)
Với p = 3 => 23 + 32 = 17 (loại)
Nhận thấy với p > 3 => p lẻ
Đặt p = 3k + 1 ; p = 3k + 2 (k \(\in Z^+\))
Khi đó P = 2p + p2
= (2p + 1) + (p2 - 1)
Vì p lẻ => 2p + 1 = (2 + 1).(2p - 1 - 2p - 2 + ... + 1) \(⋮3\)(1)
Với p = 3k + 1 => p2 - 1 = (p - 1)(p + 1) = (3k + 1 - 1)(3k + 1 + 1)
= 3k(3k + 2) \(⋮3\) (2)
Từ (1) ; (2) => P \(⋮3\)(loại)
Với p = 3k + 2 => p2 - 1 = (p - 1)(p + 1) = (3k + 2 - 1)(3k + 2 + 1)
= 3(k + 1)(3k + 1) \(⋮\)3 (3)
Từ (1) ; (3) => P \(⋮3\)
=> p = 3 là giá trị cần tìm
Dạ hay quá, em cám ơn thầy ạ
Em gặp mấy bài toán về chủ đề : Đồng Dư Thức- khó quá
May được thầy giúp đỡ ạ!

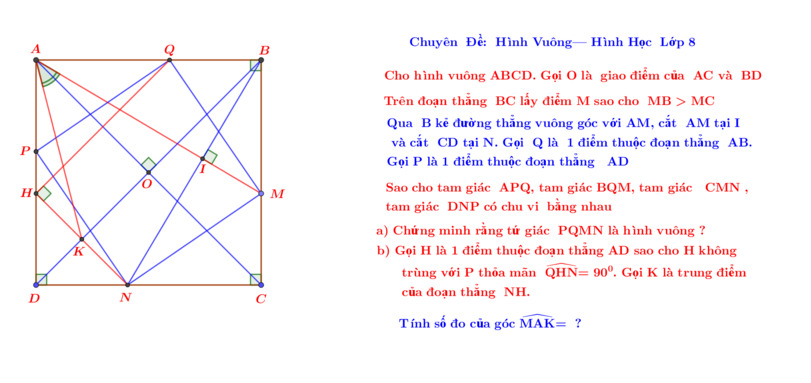
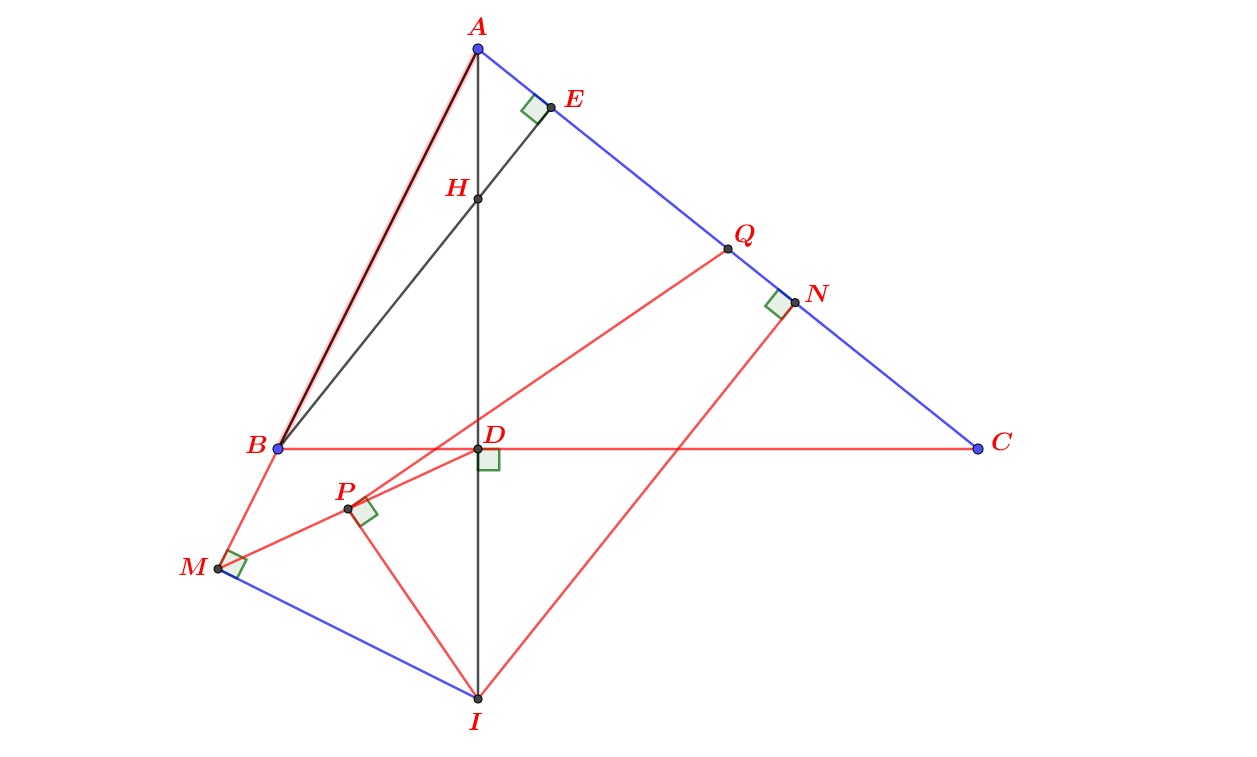
-Vì bài dài quá nên mình nói tóm tắt:
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......


Với p = 2 => 8p2 +1 = 33 (loại)
Với p = 3 => 8p2 + 1 = 73 (tm)
Với p > 3 => Đặt p = 3k + 1 ; p = 3k + 2 (k \(\in Z^+\))
Với p = 3k + 1 => 8p2 + 1 = 8(3k + 1)2 + 1
= 72k2 + 48k + 9 = 3(24k2 + 16k + 3) \(⋮3\)(loại)
Với p = 3k + 2 => 8p2 + 1 = 8(3k + 2)2 + 1
= 72k2 + 96k + 33 = 3(24k2 + 32k + 11) \(⋮3\)(loại)
Vậy p = 3 thì 8p2 + 1 \(\in P\)
- Với \(p=2\) ko thỏa mãn
- Với \(p=3\Rightarrow8p^2+1=73\) là số nguyên tố (thỏa mãn)
- Với \(p>3\Rightarrow p^2\equiv1\left(mod3\right)\)
\(\Rightarrow p^2=3k+1\)
\(\Rightarrow8p^2+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)\) là số lớn hơn 3 và chia hết cho 3
\(\Rightarrow8p^2+1\) là hợp số (ktm)
Vậy \(p=3\) là SNT duy nhất thỏa mãn yêu cầu



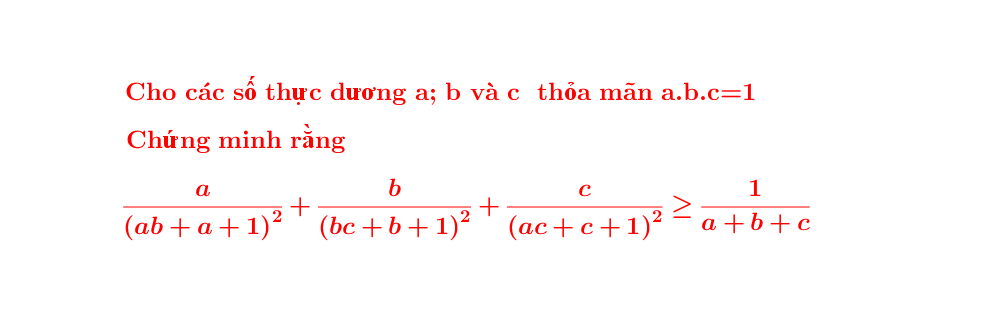


Lời giải:
Hiệu số tuổi giữa 2 anh em không đổi, tức là 5 năm trước anh cũng hơn em 5 tuổi
Coi tuổi em 5 năm trước là 1 phần thì tuổi anh 5 năm trước là 2 phần.
Hiệu số phần bằng nhau: $2-1=1$ (phần)
Tuổi em 5 năm trước: $5:1\times 1=5$ (tuổi)
Tuổi em hiện nay: $5+5=10$ (tuổi)
Tuổi anh hiện nay: $10+5=15$ (tuổi)