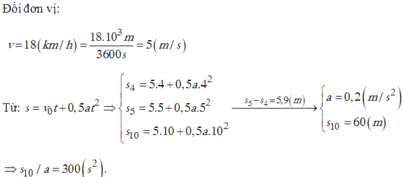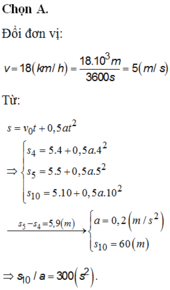1. Một vật bắt đầu chuyển động thẳng nhanh dần đều trên quãng đường 20m biết trong giây thứ sáu vật đi được quãng đường bằng 17,5cm. Tính gia tốc chuyển động của vật và thời gian vật đi hết 2 m cuối cùng trên quãng đường đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Quãng đường vật chuyển động: \(S=v_0t+\dfrac{1}{2}at^2=20t+\dfrac{1}{2}at^2\)
Vật chuyển động chậm dần đều \((a=0m/s^2)\) cho đến khi vật dừng lại \((v=0m/s)\).
\(v^2-v_0^2=2aS\Rightarrow S=\dfrac{-20^2}{2\cdot a}=-\dfrac{200}{a}\left(m\right)\)
\(\Rightarrow20t+\dfrac{1}{2}at^2=-\dfrac{200}{a}\)
Mà \(v=v_0+at=20+at=0\Rightarrow a=-\dfrac{20}{t}\)
Như vậy: \(\Rightarrow20t+\dfrac{1}{2}\cdot\left(-\dfrac{20}{t}\right)\cdot t^2=-\dfrac{200}{-\dfrac{20}{t}}\)
\(\Rightarrow t=1272,7s\)
Gia tốc vật: \(a=-\dfrac{20}{1272,7}\approx-0,0157m/s^2\)

Theo kết quả trên, ta tìm được quãng đường vật đi được sau khoảng thời gian t = 10 s là
s 10 = 5.10 + (0.2. 10 2 )/2 = 50 + 10 = 60 (m)
1 vật bắt đầu chuyển động nhanh dần đều trong giây thứ 2 vật đi được quãng đường 1,5 m//tính gia tốc

\(\Rightarrow\left\{{}\begin{matrix}S\left(3s\right)=vot+\dfrac{1}{2}at^2=\dfrac{1}{2}at^2=4,5a\\S\left(2s\right)=\dfrac{1}{2}at'^2=2a\end{matrix}\right.\)\(\Rightarrow1,5=S\left(3s\right)-S\left(2s\right)=4,5a-2a\Rightarrow a=0,6m/s^2\)