trong năm 2021-2022 học sinh a tham dự 2 lần thi thử và 1 kỳ thi tuyển sinh.Điểm môn toán (thi thử lần 1) dưới trung bình .Lần 2 do kỹ lưỡng hơn nên đã tăng 50% so với lần 1 và bằng 4/5 điểm thi tuyển sinh. Hỏi điểm thi tuyển sinh của học sinh A biết điểm thi tuyển sinh hơn 2,5 điểm so với trung bình của hai lần thi thử đó ? Mọi người giúp em với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đổi : 1/4=25%
số học sinh dự thi lý chiếm số phần trăm là :
100%-60%-25%=15%
số học sinh dự thi của trường đó là :
30:15x100=200(học sinh)
số học sinh dự thi môn anh và toán là :
200:100x60=120(học sinh)
số học sinh dự thi toán là :
(120+20):2=70(học sinh)
30 em chiếm số phần là : 100%-60%-1/4= 1/4
độ tuyển của trường có số em là: 30:1/4 =120 em
số học sinh thi toán là: 120 . 60%=72
k mình nha

a: Số học sinh dự thi môn Văn chiếm: 1/3*5/4=5/12(tổng số)
=>Số học sinh thi Ngoại Ngữ chiếm:
2/3-5/12=3/12=1/4(tổng số)
Tổng số học sinh dự thi là:
12:1/4=48(bạn)
b: Số học sinh đỗ đội tuyển là:
48*5/12*2=20*2=40 bạn
=>Tỉ số phần trăm là 40/48=5/6=83,33%

Trường hợp 1 : Trường đại học chỉ xét 1 trong 2 môn Toán hoặc Văn :
Có : \(2.C_6^2=30\) cách
Trường hớp 2 : Trường đại học xét cả 2 môn Toán và Văn :
Có : \(1.C_6^2=6\) cách
Vậy có các trường hợp là : 30+6=36 cách

Chọn A.
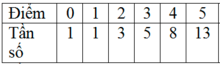
Do kích thước mẫu N = 100 là một số chẵn nên số trung vị là trung bình cộng của 2 giá trị đứng thứ 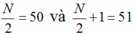
do đó 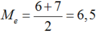

Tóm tắt:
Số huy chương vàng:
Năm 2017: 4 huy chương
Sau 43 năm: ít hơn 10 lần số huy chương năm 2017 là 1 chiếc.
Hỏi: Sau 43 năm ? huy chương vàng?
Số huy chương bạc:
Năm 2017: 1 huy chương
Sau 43 năm: gấp 17 lần số huy chương năm 2017
Hỏi: Sau 43 năm có ? huy chương bạc?
Giải:
Số huy chương vàng đội tuyển quốc gia đạt được sau 43 năm là:
10 x 4 – 1 = 39 (huy chương)
Số huy chương bạc đội tuyển quốc gia đạt được sau 43 năm là:
1 x 17 = 17 (huy chương)
Đáp số: 39 huy chương vàng; 17 huy chương bạc

Đáp án C
Không gian mẫu là cách chọn môn tự chọn và số mã đề thi có thể nhận được của An và Bình.
• An có C 3 2 cách chọn hai môn tự chọn, có C 8 1 . C 8 1 mã đề thi cỏ thể nhận cho 2 môn tự chọn của An.
• Bình giống An. Nên số phần tử của không gian mẫu là n Ω = C 3 2 . C 8 1 . C 8 1 =36864.
Gọi X là biến cổ “ An và Bình có chung đúng một môn thi tự chọn và chung một mã đề”
Số cách chọn môn thi tự chọn của An và Bình là C 3 1 . 2 ! = 6 .
Trong mồi cặp để mà đề cùa An và Bình giống nhau khi An và Bình cùng mã đề của môn chung, với mỗi cặp có cách nhận mã đề cua An và Bình là C 3 2 . C 8 1 . C 8 1 = 512
Do đó, số kết quả thuận lợi của biến cố X là n X = 6 . 512 = 3072 .
Vây xác suât cân tính là P = n X n Ω = 3072 36864 = 1 12 .

Gọi điểm thi tuyển sinh là x
=>Điểm thi lần 2 là: 0,8x
ĐIểm thi lần 1 là: 0,8x*2/3=8/15x
Theo đề, ta có: x=1/2(0,8x+8/15x)+2,5
=>x=0,4x+4/15x+2,5
=>2/3x+2,5=x
=>-1/3x=-2,5
=>x=7,5