Một người đi xe đạp dự định đi từ thành phố A đến thành phố B cách nhau 36 km trong một thời gian nhất định. Đi được nửa đường người đó nghỉ 18 phút, nên để đến B đúng hẹn người đó phỉa tăng vân tốc thêm 2 km/h trên quãng đường còn lại. Tính vận tốc ban đầu.
Mọi người giúp mình với!!!!

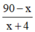 (h).
(h).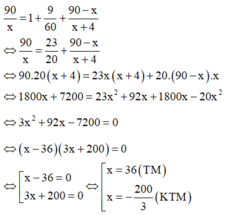
gọi vận tốc bạn đầu là: x (km/h; x>0); thời gian đến B dự định: 36/x
=> vận tốc nửa đường cong lại: x+2
36:2=18 km. đổi: 18'=3/10 h
thời gian đi nửa S đầu: 18/x (h)
thời gian đi nửa S sau: 18/x+2
vì người đó đến B đúng với dự định nên ta có pt:
\(\frac{18}{x}+\frac{18}{x+2}+\frac{3}{10}=\frac{36}{x}\Leftrightarrow\frac{18x+36+18x-36x-72}{x\left(x+2\right)}=-\frac{3}{10}\Leftrightarrow-3x^2-6x+360=0\)
\(\Leftrightarrow x^2+2x-120=0\Leftrightarrow\left(x-10\right)\left(x+12\right)=0\)
=> x=10 (t/m đk) hoặc x=-12 (k t/m đk)
=> vận tốc dđ là: 10 km/h