Cho tam giác ABC cân tại A kẻ AH vuông góc với BC ( H thuộc BC )
a) chứng minh tam giác ABH = tam giác ACH
b) Gọi N là trung điểm của AC hai đoạn thẳng BN và AH cắt nhau tại G trên tia đối của tia NB lấy K sao cho NK = NG
chứng minh G là trọng tâm của tam giác ABC và AG // CK
c) chứng minh G là trung điểm BK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tg AHB và tg AHC, có:
AB=AC(tg cân)
góc AHB= góc AHC(=90o)
AH chung.
=>tg AHB= tg AHC( ch-cgv)
=>BH=HC.
=>H là trung điểm của BC.

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
b: Sửa đề: Trên tia đối của tia HA
Xét ΔABH vuông tại H và ΔDCH vuông tại H có
HA=HD
HB=HC
Do đó: ΔABH=ΔDCH
c: Sửa đề: Cm ΔACD cân
Ta có: ΔABH=ΔDCH
=>DC=AB
mà AB=AC
nên CA=CD
=>ΔCAD cân tại C

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔAHC
Suy ra: BH=CH
hay H là trung điểm của BC
b: Xét ΔABH vuông tại H và ΔDCH vuông tại H có
HB=HC
HA=HD
Do đó: ΔABH=ΔDCH
c: Ta có: ΔABH=ΔDCH
nên AB=DC
mà AB=AC
nên DC=AC
hay ΔACD cân tại C

ghhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh
mấy bạn bớt nhắn linh tinh lên đây đi, olm là nơi học bài và hỏi bài chứ không phải nhắn lung tung

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
mà B,H,C thẳng hàng(gt)
nên H là trung điểm của BC(Đpcm)
b) Xét ΔAMB và ΔCME có
\(\widehat{AMB}=\widehat{CME}\)(hai góc đối đỉnh)
MA=MC(M là trung điểm của AC)
\(\widehat{BAM}=\widehat{ECM}\)(hai góc so le trong, AB//CE)
Do đó: ΔAMB=ΔCME(g-c-g)
Xét ΔABC có
BM là đường trung tuyến ứng với cạnh AC(M là trung điểm của AC)
AH là đường trung tuyến ứng với cạnh BC(H là trung điểm của BC)
BM cắt AH tại I(gt)
Do đó: I là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)

a)xét 2 tam giác vuông ABH và tam giác ACH có:
AB=AC(GT)
góc ABH=góc ACH(GT)
\(\Rightarrow\) tam giácABH = tam giác ACH(cạnh huyền-góc nhọn)
b)xét 2 tam giác ANG và tam giác CNK có:
CN=AN(GT)
góc KNC=góc ANG(2 góc đối đỉnh)
GN=KN(GT)
\(\Rightarrow\)tam giác ANG=tam giác CNK(c-g-c)
\(\Rightarrow\)Góc GAN=góc KCN
Vì góc GAN=góc KCN,mà 2 góc này ở vị trí so le trong
\(\Rightarrow\)AH//CK


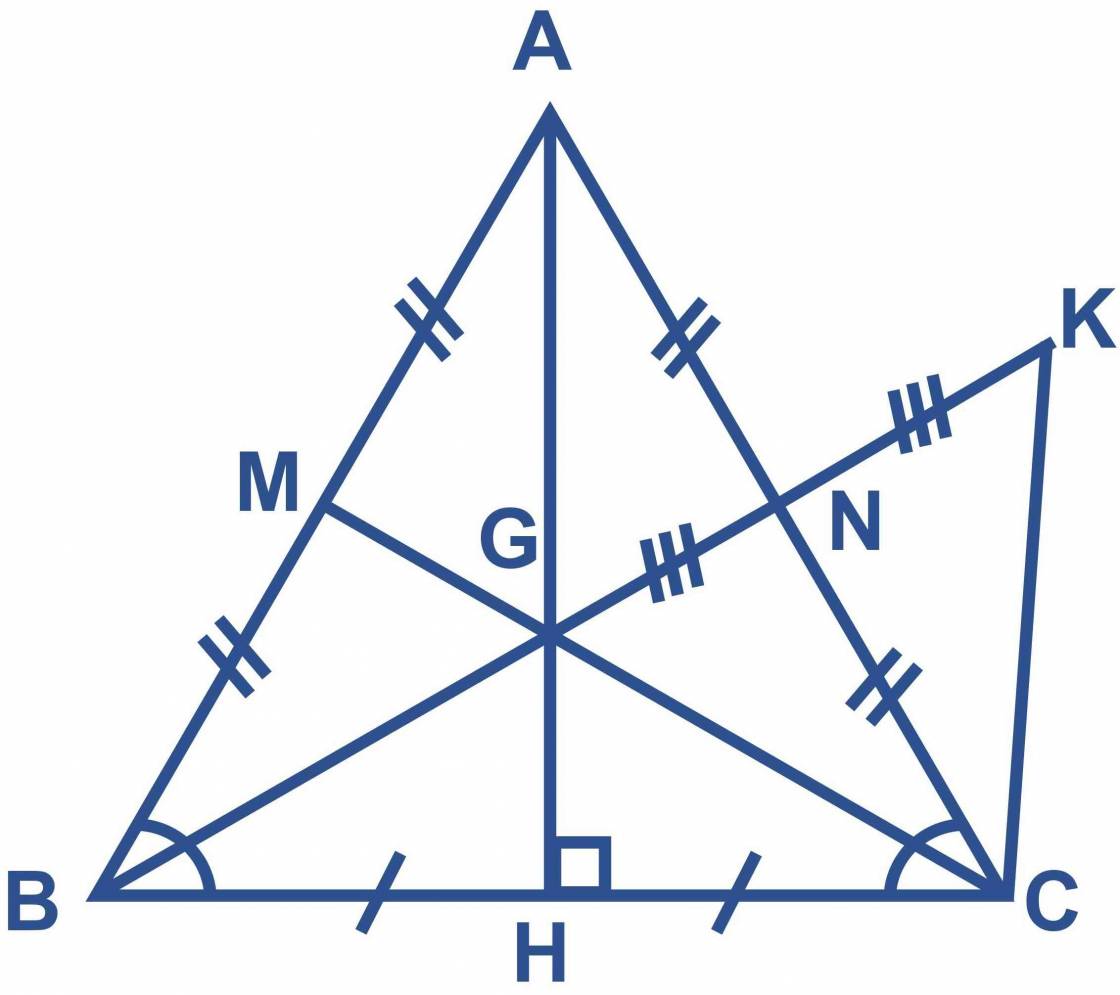
a) trong ΔABC, có góc AHB là góc vuông
góc ABH là góc nhọn
⇒ góc AHB > góc ABH
⇒ AB > AH
b) M là trung điểm của AB và N là trung điểm của AC, mà AB = AC (2 cạnh bên của tam giác cân) ⇒ MB = NC
xét tam giác MBC và tam giác NCB, ta có :
MB = NC (cmt)
góc B = góc C (2 góc đáy của 1 tam giác cân)
BC là cạnh chung
⇒ tam giác MBC = tam giác NCB (c-g-c)
⇒ MC = NB (2 cạnh tương ứng)
c) xét tam giác NAG và tam giác NCK , ta có :
NA = NC (vì N là trung điểm của cạnh AC)
góc NAG = góc NCK (đối đỉnh)
NG = NK (gt)
=> tam giác NAG = tam giác NCK (c-g-c)
=> AG = CK (2 cạnh tương ứng)
Tự kẻ hình nha
a) - Vì tam giác ABC cân tại A (gt)
=> AB = AC (định nghĩa)
góc ABC = góc ACB (dấu hiệu)
- Vì AH vuông góc với BC (gt)
=> tam giác ABH vuông tại H (tc)
tam giác ACH vuông tại H (tc)
- Xét tam giác vuông ABH và tam giác vuông ACH, có:
+ AB = AC (cmt)
+ Chung AC
=> tam giác vuông ABH = tam giác vuông ACH (cạnh huyền - cạnh góc vuông)
b) - Vì tam giác vuông ABH = tam giác vuông ACH (cmt)
=> BH = CH (2 cạnh tương ứng)
=> AH là đường trung tuyến tam giác ABC (dấu hiệu)
- Vì N là trung điểm của AC (gt)
=> BN là đường trung tuyến tam giác ABC (dấu hiệu)
Mà G là giao điểm của BN và AH (gt)
=> G là trọng tâm của tam giác ABC (tc)
- Xét tam giác ANG và tam giác CNK, có:
+ NG = NK (gt)
+ AN = CN (N là trung điểm của AC)
+ góc ANG = góc CNG (đối đỉnh)
=> tam giác ANG và tam giác CNK (cgc)
=> góc AGN = góc CKN (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
=> AG // CK (dấu hiệu)
c) - Vì G là trọng tâm của tam giác ABC (cmt)
=> BG = 2/3 BN (tc)
=> NG = 1/3 BN
Mà NK = NG (gt)
=> NK = 1/3 BN
=> NK + NG = 1/3 BN + 1/3 BN
=> GK = 2/3 BN
Mà BG = 2/3 BN (cmt)
=> GK = BG
=> G là trung điểm BK