Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Xét ΔAEC và ΔAFB có:
BÂC chung
Góc BFA= CEA (= 90o)(gt)
====> ΔAEC ∼ ΔAFB (g.g) (10
b, Từ (1) ==> \(\frac{AE}{AF}\)=\(\frac{AC}{AB}\) (Định nghĩa Δ đồng dạng)==> \(\frac{AE}{AC}\)=\(\frac{AF}{AB}\)
Xét ΔAEF và ΔACB có:
\(\frac{AE}{AC}\)=\(\frac{AF}{AB}\)(Chứng minh trên)
BÂC chung
====> ΔAEF ∼ΔACB (c.g.c)
Câu c+d mình chưa làm đc
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E co
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE;AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC
a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{DAB}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABH}\) chung
Do đó: ΔABC\(\sim\)ΔHBA(g-g)
Suy ra: \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)(Các cặp cạnh tuong ứng tỉ lệ)
hay \(AB^2=BH\cdot BC\)(đpcm)
b) Xét ΔCHA vuông tại H và ΔAHB vuông tại H có
\(\widehat{HAC}=\widehat{HBA}\left(=90^0-\widehat{C}\right)\)
Do đó: ΔCHA\(\sim\)ΔAHB(g-g)
Suy ra: \(\dfrac{CA}{AB}=\dfrac{HA}{HB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AC}{HA}=\dfrac{AB}{BH}\)(1)
Xét ΔHBA có BI là đường phân giác ứng với cạnh AH(gt)
nên \(\dfrac{IA}{IH}=\dfrac{AB}{BH}\)(2)
Từ (1) và (2) suy ra \(\dfrac{IA}{IH}=\dfrac{AC}{HA}\)(3)
c) Xét ΔAHC có AK là đường phân giác ứng với cạnh CH(gt)
nên \(\dfrac{CK}{KH}=\dfrac{AC}{HA}\)(4)
Từ (3) và (4) suy ra \(\dfrac{CK}{KH}=\dfrac{AI}{IH}\)
hay KI//AC(Định lí Ta lét đảo)
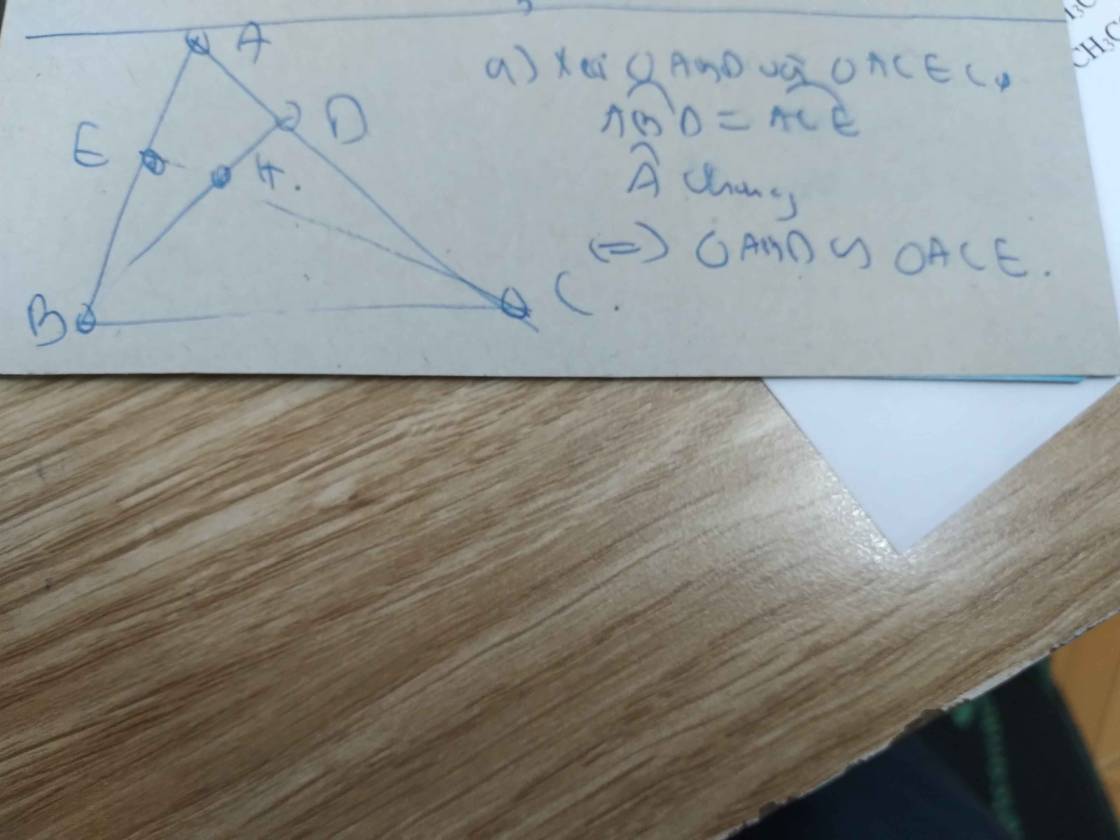
a: Xet ΔAFB vuông tại F và ΔAEC vuông tại E có
góc A chung
=>ΔAFB đồng dạng với ΔAEC
b: ΔAFB đồng dạng với ΔAEC
=>AF/AE=AB/AC
=>AF*AC=AB*AE
=>AF/AB=AE/AC
=>ΔAFE đồng dạng với ΔABC
c: Xét ΔBDH vuông tại D và ΔBFC vuông tại Fco
góc DBH chung
=>ΔBDH đồng dạng với ΔBFC