cho hàm số y = 2x2. hàm số đồng biến khi nào, nghịch biến khi nào
cho hàm số y = -3x2 hàm số đồng biến khi nào, nghịch biến khi nào
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vẽ hình:
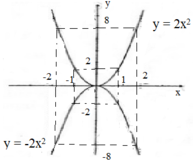
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.

a) Hàm số đồng biến khi a > 0
b) Hàm số nghịch biến khi a < 0

Vẽ hình:
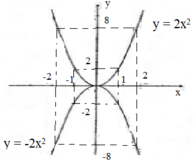
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.


Hàm số bậc nhất y=ã+b xác định với mọi giá trị của x thuộc R và có tính chất sau :
Đồng biến trên R khi a>0
Nghịch biến trên R khi a < 0
Mình cũng đang thắc mắc. Nhờ có bạn Hà Ngọc Toàn. cảm ơn bạn nha!

a) Hàm số đồng biến khi a > 0
b) Hàm số nghịch biến khi a < 0
Chúc bạn học tốt~
1. Định nghĩa
Hàm số bậc nhất là hàm số có công thức: y=ax+by=ax+b trong đó aa và bb là các số đã cho với a≠0,xa≠0,x là biến số.
2. Sự biến thiên
Hàm số bậc nhất y=ax+b(a≠0)y=ax+b(a≠0) có tập xác định D=RD=R, đồng biến trên RR nếu a>0a>0 và nghịch biến trên RR nếu a<0a<0.

1: Hàm số (1) đồng biến khi x>0, nghịch biến khi x<0
Hàm số (2) đồng biến khi x<0; nghịch biến khi x>0

a) Hàm số đồng biến khi a > 0
b) Hàm số nghịch biến khi a < 0
