Câu 12: Trong mặt phẳng tọa độ, cho A(-1;-3),B(-3;5). a. Viết phương trình tham số của đường thẳng AB. b. Viết phương trình đường tròn đường kính AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(1); vecto u=2*vecto a-vecto b
=>\(\left\{{}\begin{matrix}x=2\cdot1-0=2\\y=2\cdot\left(-4\right)-2=-10\end{matrix}\right.\)
(2): vecto u=-2*vecto a+vecto b
=>\(\left\{{}\begin{matrix}x=-2\cdot\left(-7\right)+4=18\\y=-2\cdot3+1=-5\end{matrix}\right.\)
(3): vecto a=2*vecto u-5*vecto v
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\cdot\left(-5\right)-5\cdot0=-10\\b=2\cdot4-5\cdot\left(-3\right)=15+8=23\end{matrix}\right.\)
(4): vecto OM=(x;y)
2 vecto OA-5 vecto OB=(-18;37)
=>x=-18; y=37
=>x+y=19

Đáp án C
HD: Gọi H(1+2t;-1+t;2-t) là hình chiếu của A trên d
![]()
![]()
Suy ra H(3;0;1), phương trình đường thẳng AH là
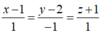
![]()

Câu 1:
a: \(A=4\sqrt{24}-3\sqrt{54}+5\sqrt{6}-\sqrt{150}\)
\(=4\cdot2\sqrt{6}-3\cdot3\sqrt{6}+5\sqrt{6}-5\sqrt{6}\)
\(=8\sqrt{6}-9\sqrt{6}=-\sqrt{6}\)
b: \(B=\sqrt{14+4\cdot\sqrt{10}}-\dfrac{1}{\sqrt{10}+3}\)
\(=\sqrt{10+2\cdot\sqrt{10}\cdot2+4}-\dfrac{\left(\sqrt{10}-3\right)}{10-9}\)
\(=\sqrt{\left(\sqrt{10}+2\right)^2}-\sqrt{10}+3\)
\(=\sqrt{10}+2-\sqrt{10}+3=5\)
Câu 2:
a:
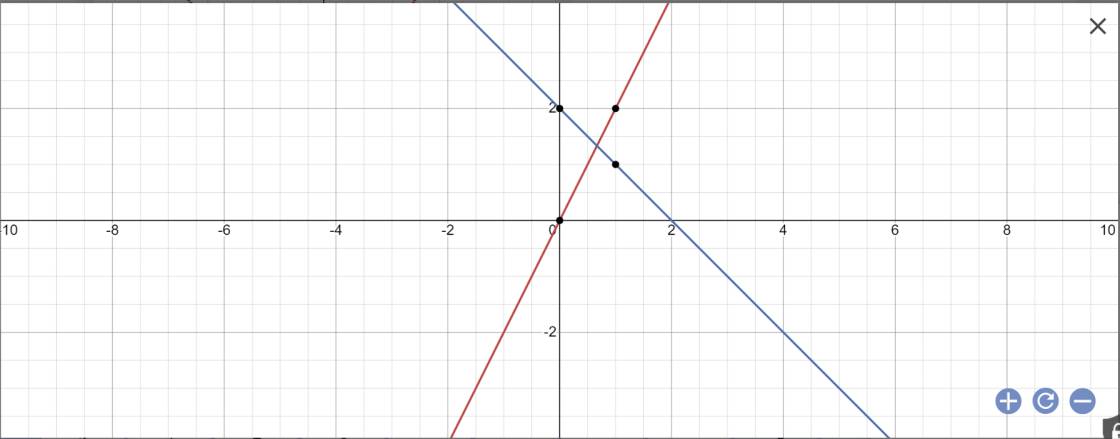
b: Vì (d3)//(d2) nên \(\left\{{}\begin{matrix}a=-1\\b\ne2\end{matrix}\right.\)
Vậy: (d3): y=-x+b
Thay x=1 vào (d1), ta được:
\(y=2\cdot1=2\)
Thay x=1 và y=2 vào y=-x+b, ta được:
b-1=2
=>b=3
vậy: (d3): y=-x+3

Lời giải:
Gọi tọa độ $M$ là $(a,0)$. $H$ là trung điểm của $MB$
Khi đó $H$ có tọa độ \(H(\frac{a-1}{2}, \frac{1}{2})\)
\(\overrightarrow{MB}=(-1-a,1); \overrightarrow{AH}=(\frac{a-3}{2}, \frac{-3}{2})\)
Vì $MAB$ cân tại $A$ nên trung tuyến $AH$ đồng thời là đường cao. Do đó:
\(\overrightarrow{MB}.\overrightarrow{AH}=0\Leftrightarrow (-1-a).\frac{a-3}{2}-\frac{3}{2}=0\Leftrightarrow a=0\) hoặc $a=2$
(đều thỏa mãn)
Khi đó:
$OM=0$ hoặc $OM=2$
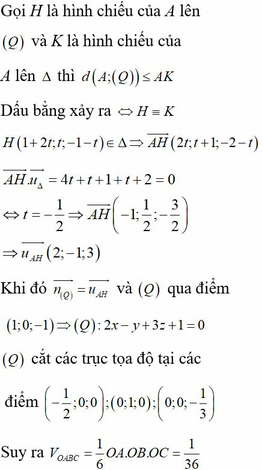

\(AB\left\{{}\begin{matrix}quaA\left(-1;-3\right)\\VTCP\overrightarrow{AB}=\left(-2;8\right)\end{matrix}\right.\)
\(PTTS\) của \(AB:\left\{{}\begin{matrix}x=-1-2t\\y=-3+8t\end{matrix}\right.\)
Gọi \(I\left(x_I;y_I\right)\) là tâm đường tròn
\(I\) là trung điểm \(AB\)
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-1-3}{2}=-2\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{-3+5}{2}=1\end{matrix}\right.\)
\(\Rightarrow I\left(-2;1\right)\)
\(AB=\sqrt{\left(-2\right)^2+8^2}=2\sqrt{17}\)
Mà \(R=\dfrac{AB}{2}=\dfrac{2\sqrt{17}}{2}=\sqrt{17}\)
Vậy \(PT\left(C\right):\left(x+2\right)^2+\left(y-1\right)^2=17\)
Coi lại bán kính.