gieo một con xúc xắc ba lần. xác suất để trong ba lần gieo có ít nhất 2 lần xuất hiện mặt có số chấm là chẵn Giúp em với ạ. Em đang cần gấp ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: n(omega)=50
n(A)=5
=>P(A)=5/50=1/10
b: n(B)=12+10+5=22+5=27
=>P(B)=27/50

Đáp án B
Phương pháp:
Phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có nghiệm
⇔ ∆ ≥ 0

![]()
![]()
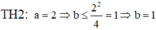
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Gọi A là biến cố:
"Phương trình a x 2 + b x + c = 0 có nghiệm"
![]()
![]()

a) Nếu gieo một xúc xắc 11 lần liên tiếp, có 5 lần xuất hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện mặt 2 chấm bằng: \(\dfrac{5}{11}\)
b) Nếu gieo một xúc xắc 14 lần liên tiếp, có 3 lần xuất hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện mặt 6 chấm bằng: \(\dfrac{3}{14}\)

Không gian mẫu trong trò chơi trên là tập hợp \(\Omega = \left\{ {(i,j)|i,j = 1,2,3,4,5,6} \right\}\)trong đó (i,j) là kết quả “Lần thứ nhất xuất hiện mặt i chấm, lần thứ hai xuất hiện mặt j chấm”. Vậy \(n(\Omega ) = \;36.\)
a) Gọi A là biến cố “Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10”.
Các kết quả có lợi cho A là: (4; 6) (5;5) (5;6) (6; 4) (6;5) (6;6). Vậy \(n(A) = \;6.\)
Vậy xác suất của biến cố A là \(P(A) = \;\frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{36}} = \frac{1}{6}.\)
b) Gọi B là biến cố “Mặt 1 chấm xuất hiện ít nhất một lần”.
Các kết quả có lợi cho B là: (1; 1) (1 : 2) (1 : 3) (1; 4) (1;5) (1; 6) (2 ; 1) (3;1) (4; 1) (5;1) (6;1). Vậy \(n(B) = \;11.\)
Vậy xác suất của biến cố B là: \(P(B) = \;\frac{{n(B)}}{{n(\Omega )}} = \frac{{11}}{{36}}.\)
Có thể là 2 lần chẵn 1 lần lẻ hoặc cả 3 lần đều chẵn
TH1: 2 chẵn, 1 lẻ
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
TH2: 3 lần đều chẵn
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
=>Có 27+27=54 cách
n(omega)=6*6*6=216
=>P=54/216=1/4