Các bạn giải hộ mình bài này nhé http://olm.vn/hỏi-đáp/question/264598.html

Tam giác ABC có: góc BAC+góc ABC+góc ACB=180^o=>60^o+góc ABC+góc ACB=180^o​

=> góc ABC+góc ACB=120^o​

góc ABM=góc MBC=1/2 góc ABC (vì BM là tia phân giác góc ABC)

góc ACN=góc NCB=1/2 góc ACB (vì CN là tia phân giác góc ACB)

=>góc ABM+góc ACN=góc MBC+góc NCB=1/2 góc ABC+1/2 góc ACB=1/2(góc ABC+góc ACB)=(1/2).120^o=60^o

góc BIC+góc IBC+góc ICB=180^o=>góc BIC+60^o=180^o=>góc BIC=120^o

góc BIN kề bù với góc BIC => góc BIN+góc BIC=180^o=>góc BIN+120^o=180^o=>góc BIN=60^o

a) từ I kẻ IK sao cho KIB=NIB(K thuộc BC)

xét tam giác INB và tam giác IKB có:

NBI=CBI(gt)

IB(chung)

NIB=IKB

suy ra tam giác INB=IKB(g.c.g)

suy ra NIB=BIC

CM tương tự ta có tam giác MIC=KIC(c.g.c)suy ra MIC=KIC

mà NIB=MIC suy ra NIB=BIK=KIC=180/3=60 độ

suy ra BIN=60 độ

a) từ I kẻ IK sao cho KIB=NIB(K thuộc BC)

xét tam giác INB và tam giác IKB có:

NBI=CBI(gt)

IB(chung)

NIB=IKB

suy ra tam giác INB=IKB(g.c.g)

suy ra NIB=BIC

CM tương tự ta có tam giác MCI=KCI(c.g.c)suy ra MIC=KIC

mà NIB=MIC suy ra BIN=BIK=CIK=180/3=60 độ

suy ra BIN=60 độ

nhanh lên mình cần gấp lắm

giúp mình với huhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhuhu

Chịu lớp6

Chịu

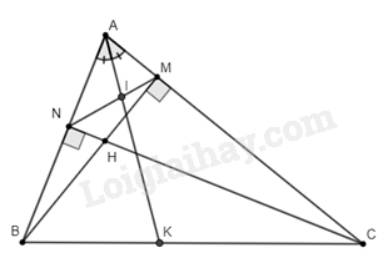
a) Vì \(BM\)là đường cao nên \(\widehat {AMB} = 90^\circ \); vì \(CN\)là đường cao nên \(\widehat {ANC} = 90^\circ \)

Xét tam giác \(AMB\) và tam giác \(ANC\) có:

\(\widehat A\) (chung)

\(\widehat {ANB} = \widehat {ANC} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta AMB\backsim\Delta ANC\) (g.g).

Suy ra, \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).

Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (tỉ lệ thức)

Xét tam giác \(AMN\) và tam giác \(ABC\) có:

\(\widehat A\) (chung)

\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (chứng minh trên)

Suy ra, \(\Delta AMN\backsim\Delta ABC\) (c.g.c).

b) Xét tam giác \(AMN\) có \(AI\) là đường phân giác của \(\widehat {MAN}\left( {I \in MN} \right)\).

Theo tính chất đường phân giác ta có:

\(\frac{{IM}}{{IN}} = \frac{{AM}}{{AN}}\)

Xét tam giác \(ABC\) có \(AK\) là đường phân giác của \(\widehat {BAC}\left( {K \in BC} \right)\).

Theo tính chất đường phân giác ta có:

\(\frac{{BK}}{{KC}} = \frac{{AB}}{{AC}}\)

Mà \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (chứng minh trên) nên \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\) (điều phải chứng minh).

Không mất tính tổng quát; giả sử ^ABC > ^ACB

Dựng K là đỉnh thứ tư của hình bình hành BMKN => ^NBM = ^NKM = ^CBM (1)

Khi đó: ^ABC > ^ACB => 1/2.^ABC > 1/2.^ACB => ^CBM > ^BCN = ^NCM  (2)

Từ (1) và (2) => ^NKM > ^NCM  (*)

Xét \(\Delta\)CMB và \(\Delta\)BNC có: Cạnh BC chung; ^CBM > ^BCN (cmt); BM = CN => CM > BN (3)

Ta có: Tứ giác BMKN là hình bình hành => BN = MK (4)

Từ (3) và (4) => CM > MK

Trong \(\Delta\)CKM có: CM > MK (cmt) => ^MKC > ^MCK (**)

Từ (*) và (**) => ^NKM + ^MKC > ^NCM + ^MCK => ^NKC > ^NCK 

Xét \(\Delta\)CNK có: ^NKC > ^NCK => CN > NK. Mà NK = BM (Do tứ giác BMKN là hbh) 

Nên CN > BM. Lại có: CN = BM (theo gt)  ---> Mâu thuẫn ---> Giả sử sai

Tiếp theo bn giả sử ^ABC < ^ACB; c/m tương tự rồi chỉ ra nó vô lí

Từ đó suy ra: ^ABC = ^ACB => \(\Delta\)ABC cân tại A (đpcm).

a)Vì trung trực của AC cắt BC tại M=>MA+MC =>Tam giác MAC cân tại M mà có góc đáy bằng góc C mà góc C là góc đáy của tam giác cân tại A=>AMC=BAC(Hai góc ở đỉnh của hai tam giác cân)
b)Xét tam giác CAN và tam giác ABM có:
AB=AC(gt)
MB=AN(gt)
Mà NAC=C+A(vì góc MAC=góc A)
ABM=C+A
=>NAC= ABM
=>Tam giác CAN=tam giác ABM(c.g.c)
=>MA=NC mà MA=MC(c/m trên)=>CM=NC
c)Thêm điều kiện góc A=45⁰

A) Vì trung trực của AC cắt BC tại M ==> Tam giác MAC cân tại M mà nó lại có góc đáy bằng góc C mà góc C lại là góc đáy của tam giác cân tại A ==> AMC = BAC(Hai góc ở đỉnh của hai tam giác cân)

B) Xét tam giác CAN và tam giác ABM có:

AB = AC (gt)

MB = AN (gt)

Mà NAC = C + A (vì góc MAC bằng với góc A)

ABM = C + A

- NAC = ABM

- Tam giác Can = Tam giác ABM (c.g.c)

MA = NC mà MA = CM (c/m trên) ==> CM = NC

C)Thêm điều kiện góc phải là 45⁰