Tìm số tự nhiên n để n-2/3n+7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VD
15 tháng 6 2023
Gọi UCLN(n-2, 3n+7) = d (d∈N*)
=> n-2 ⋮ d => 3(n-2)⋮d => 3n-6 ⋮ d
3n+7 ⋮ d
=> (3n+7)-(3n-6)⋮d => 13⋮d
Do d ∈ N* => d = 1; 13
Xét d = 13
=> n-2⋮13 => n chia 13 dư 2
Để n-2/3n+7 tối giản thì d=1 => d≠13
Vậy n-2/3n+7 tối giản khi n không chia 13 dư 2
15 tháng 6 2023
Đặt `d=(n-2,3n+7)` với `d\inNN^(**)`
`=>{(n-2\vdots d),(3n+7\vdots d):}`
`=>3n+7-3(n-2)\vdotsd`
`<=>13\vdots d=>d\in Ư(13)={1;13}`
Để `(n-2)/(3n+7)` là phân số tối giản `=>d\ne13`
hay `n-2\cancel(\vdots)13`
`=>n\ne13k+2(k\inNN)`
Vậy `n\ne 13k+2` với `k` là số tự nhiên tuỳ ý
NT
a, Tìm cặp số tự nhiên x,y biết (x-2) .(y + 7) =17
b,Tìm số tự nhiên n để ( 3n+16) chia hết cho (n+4)
1
NM
Nguyễn Minh Quang
Giáo viên
7 tháng 12 2021
ta có y+7 là số tự nhiên lớn hơn 7 và là ước của 17
thế nên \(\hept{\begin{cases}y+7=17\\x-2=1\end{cases}\Leftrightarrow\hept{\begin{cases}y=10\\x=3\end{cases}}}\)
b. ta có : \(3n+14=3\times\left(n+4\right)+2\) chia hết cho n+4 khi 2 chia hết cho n+4
mà n là số tự nhiên nên n+4 > 3 thế nên không tồn tại số tự nhiên thỏa mãn
KV
19 tháng 10 2023
3n + 7 = 3n - 3 + 10 = 3(n - 1) + 10
Để (3n + 7) ⋮ (n - 1) thì 10 ⋮ (n - 1)
⇒ n - 1 ∈ Ư(10) = {-10; -5; -2; -1; 1; 2; 5; 10}
⇒ n ∈ {-9; -4; -1; 0; 2; 3; 6; 11}
Mà n là số tự nhiên
⇒ n ∈ {0; 2; 3; 6; 11}
PD
0
NT
0
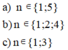
Để `(n+2)/(3n+7)` là sao?
là bn phải đi tìm cái số n nớ đó bn