Trong World Cup 2022 được tổ chức ở Qatar, quả bóng được sử dụng cho các trận đấu có dạng hình cầu và có đường kính bằng 22cm. Tính diện tích bề mặt của quả bóng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Một quả bong tennis có dạng hình cầu, người ta đo được chu vi của dường tròn bao quanh quả bóng là 20,41cm. Vậy một đựng bóng tennis cao 19,5cm có thể chứa nhiều nhất bao nhiêu quả bóng ten-nít? lớp 5 help tui

\(v_0=0\)m/s; \(v=100,8\)km/h=28m/s
Gia tốc vật:
\(v=v_0+at\Rightarrow a=\dfrac{v}{t}=\dfrac{28}{0,04}=700\)m/s2

| Loại bóng | Quả bóng gôn | Quả khúc côn cầu | Quả ten-nit | Quả bóng bàn | Quả bi-a |
| Đường kính | 42,7mm | 7,32cm | 6,5cm | 40mm | 61mm |
| Độ dài đường tròn lớn | 134,08mm | 23cm | 20,41cm | 125,6mm | 171,71mm |
| Diện tích | 57,25cm2 | 168,25cm2 | 132,67cm2 | 5024mm2 | 11683,94mm2 |
| Thể tích | 40,74cm3 | 205,26cm3 | 143,72cm3 | 33,49 cm3 | 118,79cm3 |
Cách tính:
+ Quả bóng gôn:
d = 42,7mm ⇒ R = d/2 = 21,35 mm
⇒ Độ dài đường tròn lớn: C = 2π.R=2.3,14.21,35 ≈ 134,08 (mm)
⇒ Diện tích mặt cầu: S = πd2 = 3,14.(42,7)2 ≈ 5725 mm2 = 57,25 (cm2).
⇒ Thể tích khối cầu: 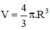
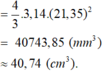
+ Quả khúc côn cầu:
C = πd = 23cm ⇒ 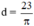 ≈ 7,32 (cm)
≈ 7,32 (cm)
⇒ Diện tích mặt cầu: S = πd2=3,14.(7,32)2 = 168,25 (cm2).
⇒ Thể tích khối cầu: 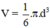
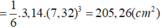
+ Quả ten-nít:
d = 6,5cm
⇒ Độ dài đường tròn lớn: C = π.d = 3,14.6,5 = 20,41 (cm)
⇒ Diện tích mặt cầu: S = πd2= 3,14.(6,5)2=132,67 (cm2)
⇒ Thể tích khối cầu: 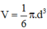
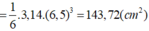
+ Quả bóng bàn:
d = 40mm
⇒ Độ dài đường tròn lớn C = π.d =3,14.40 ≈ 125,6 (mm)
⇒ Diện tích mặt cầu: S = π.d2=3,14.402 = 5024 (mm2)
⇒ Thể tích khối cầu: 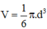
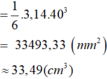
+ Quả bi-a;
d = 61mm
⇒ Độ dài đường tròn lớn C = π.d =3,14.61 = 191,54 (mm)
⇒ Diện tích mặt cầu: S = π.d2=3,14.612 ≈ 11683,94 (mm2)
⇒ Thể tích khối cầu: 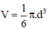
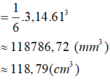

Từ công thức \(S_{cầu}=4\pi r^2=1256\left(cm^2\right)\)
\(\Rightarrow r^2=\dfrac{1256}{4\pi}\approx100\left(cm\right)\Rightarrow r\approx10\left(cm\right)\)

Giả sử căt hình đó thành 1 mặt phẳng đi qua trục của nón ta được thiết diện như hình vẽ. Trong đó tam giác ABC là tam giác đều và là thiết diện của khối nón. Hình tròn tâm I là thiết diện của quả bóng.
Ta nhận thấy tam giác ABC ngoại tiếp đường tròn tâm I
Hình nón có chiều cao là \(OH=3IH=30\) (cm)
Bán kính đáy nón là \(HA=\frac{30}{\sqrt{3}}=10\sqrt{3}\left(cm\right)\)
Thể tích khối nón là \(V_1=\frac{1}{3}OH.\pi.AH^2=\frac{1}{3}.30\pi.300=3000\pi\left(cm^3\right)\)
Thể tích phần không gian bên trong khối nón không bị quả bóng chiếm chỗ là :
\(V_2=\frac{1}{3}OH.\pi.AH^2-\frac{1}{4}\pi.IH^2=3000\pi-\frac{4000}{3}\pi=\frac{5000}{3}\pi\left(cm^3\right)\)

Chọn đáp án B
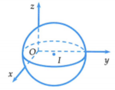
Hai bức tường và nền nhà mà quả bóng tiếp xúc tạo thành một hệ trục tọa độ Oxyz như hình vẽ. Mỗi quả bóng coi như một mặt cầu có tâm I a ; b ; c
Vì mỗi quả bóng đều tiếp xúc với hai bức tường và nền nhà nên chúng tiếp xúc với ba mặt phẳng tọa độ O x y , O y z v à O x z
Tức là
![]()
![]()
Suy ra I a ; a ; a
Gọi M x ; y ; z là điểm nằm trên quả bóng có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng 1, 2, 4
Suy ra M 1 ; 2 ; 4
Điểm M nằm trên quả bóng khi
![]()
![]()
Phương trình (*) có ∆ ' = 7 > 0 nên có hai nghiệm a 1 , a 2 và a 1 + a 2 = 7 (theo định lý Vi-ét). Khi đó tổng đường kính của hai quả bóng là
2 a 1 + a 2 = 14
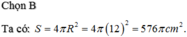
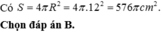


Để tính diện tích bề mặt của quả bóng, ta sử dụng công thức diện tích bề mặt của hình cầu:
Diện tích bề mặt của hình cầu = 4πr^2
Trong đó, r là bán kính của quả bóng. Với đường kính của quả bóng bằng 22 cm, ta có bán kính r = 22 cm / 2 = 11 cm.
Thay giá trị của r vào công thức, ta có:
Diện tích bề mặt của quả bóng = 4π(11 cm)^2
Diện tích bề mặt của quả bóng = 4π(121 cm^2)
Diện tích bề mặt của quả bóng ≈ 1520.53 cm^2
Vậy diện tích bề mặt của quả bóng là khoảng 1520.53 cm^2.
câu này là trong đề thi tỉnh Kiên Giang mới thi hôm qua, tui làm ra 484π nhưng khi coi đáp án thì lại là 121π nên tui mới nhờ mn xem dùm