- Giải hộ #Ngân bài này lẹ lẹ nha nha mọi người
Qua O nằm trong tam giác vẽ các đường song song với ba cạnh.Các đường thẳng chia tam giác ABC thành 3 hình bình hành và 3 tam giác nhỏ.Biết diện tích tam giác nhỏ là a^2,b^2,c^2.
a) Tính diện tích tam giác ABC
b) Chứng minh: diện tích tam giác ABC =< 3(a^2+b^2+c^2)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a.x+\dfrac{3}{7}=\dfrac{2}{5}+\dfrac{3}{10}\)
\(x+\dfrac{3}{7}=\dfrac{7}{10}\)
\(x=\dfrac{7}{10}-\dfrac{3}{7}\)
\(x=\dfrac{19}{70}\)
\(b.\dfrac{19}{20}-x=\dfrac{8}{5}-\dfrac{3}{4}\)
\(\dfrac{19}{20}-x=\dfrac{17}{20}\)
\(x=\dfrac{19}{20}-\dfrac{17}{20}\)
\(x=\dfrac{2}{20}=\dfrac{1}{10}\)


What does the mother look like?
What does the mother do?
Who is taller, the son or the daughter?
How old is the daughter?
What class is the son in?

Câu 1:
TXĐ:D=R
\(f\left(-x\right)=2\cdot\left(-x\right)^4-3\cdot\left(-x\right)^2+1\)
\(=2x^4-3x^2+1=f\left(x\right)\)
=>f(x) là hàm số chẵn

a: Số lớn là 1092*4/7=624
Số bé là 1092-624\=468
b: Số lớn là 684*7/12=399
Số bé là 684-399=285
c: Số lớn là 2184*9/14=1404
Số bé là 780
d: Số lớn là 1428*13/17=1092
Số bé là 1428-1092=336

Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm

\(A,\dfrac{9}{7}-\dfrac{6}{8}=\dfrac{72}{56}-\dfrac{42}{56}=\dfrac{30}{56}=\dfrac{15}{28}\)
\(b,\dfrac{91}{42}-\dfrac{54}{42}=\dfrac{27}{42}\)
c và d làm tương tự nhé ( mà sao dấu trừ dấu cộng bay xuống mẫu số vậy =)

Gọi số hoa của Hằng và Nga lần lượt là a,b
Theo đề, ta có: a-b=18 và a+6=5/3b
=>a-b=18 và a-5/3b=-6
=>a=54 và b=36

 ai giải hộ mik với
ai giải hộ mik với
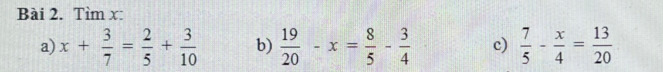




 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !

