\(\frac{x^2}{\sqrt{5}}-2\sqrt{5}=0\\ \frac{x^2}{\sqrt{5}}=2\sqrt{5}\\ \frac{x^2\sqrt{5}}{\sqrt{5}}=2\sqrt{5}.\sqrt{5}\\ x^2=10\\ x=+-\sqrt{10}\)

2)\(\sqrt{25\left(2x+1\right)^2}=0\\ 5\left(2x+1\right)=0\\ x=\frac{-1}{2}\)

a)Pt \(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=\dfrac{1}{3}+\dfrac{1}{2}\)

\(\Leftrightarrow\left|2x-1\right|=\dfrac{5}{6}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=\dfrac{5}{6}\\2x-1=-\dfrac{5}{6}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{12}\\x=\dfrac{1}{12}\end{matrix}\right.\)

Vậy...

b)Đk:\(x\ge3\)

Pt \(\Leftrightarrow\sqrt{x-3}\left(x-4\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\x-4=0\\x-2=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=4\left(tm\right)\\x=2\left(ktm\right)\end{matrix}\right.\)

Vậy...

c)Đk:\(x\ge1\)

\(x+\sqrt{x-1}=13\)

\(\Leftrightarrow\sqrt{x-1}=13-x\)

\(\Leftrightarrow\left\{{}\begin{matrix}13-x\ge0\\x-1=x^2-26x+169\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}13\ge x\\x^2-27x+170=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}13\ge x\\x^2-17x-10x+170=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}13\ge x\\\left(x-17\right)\left(x-10\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}13\ge x\\\left[{}\begin{matrix}x=17\\x=10\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow x=10\) (tm)

Vậy...

\(a,đk:x\ge5\\ \Leftrightarrow\sqrt{x-5}+\sqrt{4\left(x-5\right)}-\dfrac{1}{5}\sqrt{9\left(x-5\right)}=3\\ \Leftrightarrow\sqrt{x-5}+2\sqrt{x-5}-\dfrac{1}{5}.3\sqrt{x-5}=3\\ \Leftrightarrow\dfrac{12}{5}\sqrt{x-5}=3\\ \Rightarrow\sqrt{x-5}=\dfrac{5}{4}\\ \Leftrightarrow\left(\sqrt{x-5}\right)^2=\left(\dfrac{5}{4}\right)^2\\ \Leftrightarrow x-5=\dfrac{25}{16}\\ \Rightarrow x=\dfrac{25}{16}+5\\ \Rightarrow x=\dfrac{105}{16}\left(t|m\right)\)

\(b,đk:x\ge1\\ \Leftrightarrow\sqrt{x-1}+\sqrt{4\left(x-1\right)}-\sqrt{25\left(x-1\right)}=-2\\ \Leftrightarrow\sqrt{x-1}+2\sqrt{x-1}-5\sqrt{x-1}=-2\\ \Leftrightarrow-2\sqrt{x-1}=-2\\ \Leftrightarrow\sqrt{x-1}=1\\ \Leftrightarrow x-1=1\\ \Leftrightarrow x=2\left(t|m\right)\)

Bài 3:

a: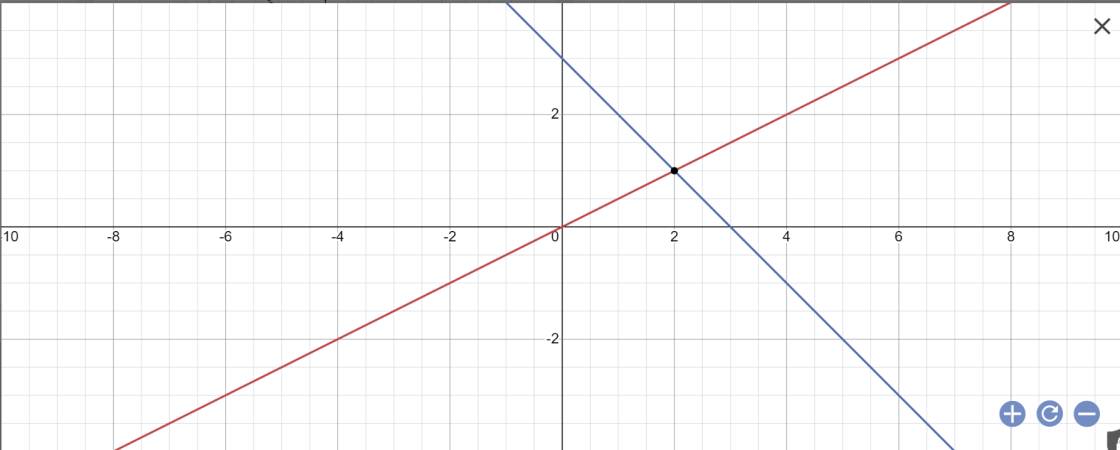 

b: Phương trình hoành độ giao điểm của (d1) và (d2) là:

\(\dfrac{1}{2}x=-x+3\)

=>\(\dfrac{1}{2}x+x=3\)

=>1,5x=3

=>x=2

Khi x=2 thì y=-x+3=-2+3=1

Vậy: (d1) cắt (d2) tại A(2;1)

c:

Đặt (d): y=ax+b(a<>0)

Vì (d)//(d2) nên a=-1 và b<>3

=>(d): y=-x+b

Thay x=4 vào (d1), ta được:

\(y=\dfrac{1}{2}\cdot4=2\)

Thay x=4 và y=2 vào (d), ta được:

b-4=2

=>b=6

Vậy: (d): y=-x+6

Bài 2:

a: ĐKXĐ: x>=2/3

\(\sqrt{3x-2}=5\)

=>\(3x-2=5^2=25\)

=>3x=25+2=27

=>x=27/3=9(nhận)

b: ĐKXĐ: \(x\in R\)

\(\sqrt{4x^2-4x+1}=1\)

=>\(\sqrt{\left(2x-1\right)^2}=1\)

=>|2x-1|=1

=>\(\left[{}\begin{matrix}2x-1=1\\2x-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=0\left(nhận\right)\end{matrix}\right.\)

Bài 1:

\(A=2\sqrt{5}-\sqrt{20}+3\sqrt{45}\)

\(=2\sqrt{5}-2\sqrt{5}+3\cdot3\sqrt{5}\)

\(=9\sqrt{5}\)

\(B=\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{\left(2+\sqrt{3}\right)^2}\)

\(=\left|2-\sqrt{3}\right|+\left|2+\sqrt{3}\right|\)

\(=2-\sqrt{3}+2+\sqrt{3}=4\)

a) Ta có: \(\sqrt{\left(x+1\right)^2}=3\)

\(\Leftrightarrow\left|x+1\right|=3\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1=3\\x+1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)

b) Ta có: \(3\sqrt{4x+4}-\sqrt{9x-9}-8\sqrt{\dfrac{x+1}{16}}=5\)

\(\Leftrightarrow6\sqrt{x+1}-3\sqrt{x-3}-2\sqrt{x+1}=5\)

\(\Leftrightarrow4\sqrt{x+1}=5+3\sqrt{x-3}\)

\(\Leftrightarrow16\left(x+1\right)=25+30\sqrt{x-3}+9\left(x-3\right)\)

\(\Leftrightarrow16x+16=25+9x-27+30\sqrt{x-3}\)

\(\Leftrightarrow30\sqrt{x-3}=16x+16+2-9x\)

\(\Leftrightarrow30\sqrt{x-3}=7x+18\)

\(\Leftrightarrow x-3=\left(\dfrac{7x+18}{30}\right)^2\)

\(\Leftrightarrow x-3=\dfrac{49x^2}{900}+\dfrac{7}{25}x+\dfrac{9}{25}\)

\(\Leftrightarrow\dfrac{49}{900}x^2-\dfrac{18}{25}x+\dfrac{84}{25}=0\)

\(\Delta=\left(-\dfrac{18}{25}\right)^2-4\cdot\dfrac{49}{900}\cdot\dfrac{84}{25}=-\dfrac{16}{75}< 0\)

Vậy: Phương trình vô nghiệm

a)Pt\(\Leftrightarrow\left|x+1\right|=3\Leftrightarrow\left[{}\begin{matrix}x+1=3\\x+1=-3\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)

b)Đk:\(x\ge-1\)

Sửa đề: \(3\sqrt{4x+4}-\sqrt{9x+9}-8\sqrt{\dfrac{x+1}{16}}=5\)

Pt \(\Leftrightarrow6\sqrt{x+1}-3\sqrt{x+1}-2\sqrt{x+1}=5\)

\(\Leftrightarrow\sqrt{x+1}=5\)

\(\Leftrightarrow x=24\left(tm\right)\)

a, \(\Leftrightarrow\left|2x-1\right|=4\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=4\\2x-1=-4\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)

Vậy ...

b, ĐKXĐ : \(x\ge-1\)

\(\Leftrightarrow2\sqrt{x+1}-3\sqrt{x+1}-2\sqrt{x+1}=5\)

\(\Leftrightarrow\sqrt{x+1}=-\dfrac{5}{3}\)

Vậy phương trình vô nghiệm

a)Pt \(\Leftrightarrow\left|2x-1\right|=4\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=4\\2x-1=-4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)

Vậy...

b)Đk:\(x\ge-1\)

Pt\(\Leftrightarrow2\sqrt{x+1}-3\sqrt{x+1}-2\sqrt{x+1}=5\)

\(\Leftrightarrow-3\sqrt{x+1}=5\) (vô nghiệm)

Vậy...

a: ĐKXĐ: x>=5

\(\sqrt{4x-20}+\sqrt{x-5}-\dfrac{1}{3}\cdot\sqrt{9x-45}=4\)

=>\(2\sqrt{x-5}+\sqrt{x-5}-\dfrac{1}{3}\cdot3\sqrt{x-5}=4\)

=>\(2\sqrt{x-5}=4\)

=>\(\sqrt{x-5}=2\)

=>x-5=4

=>x=9(nhận)

b: ĐKXĐ: x>=1/2

\(\sqrt{2x-1}-\sqrt{8x-4}+5=0\)

=>\(\sqrt{2x-1}-2\sqrt{2x-1}+5=0\)

=>\(5-\sqrt{2x-1}=0\)

=>\(\sqrt{2x-1}=5\)

=>2x-1=25

=>2x=26

=>x=13(nhận)

c: \(\sqrt{x^2-10x+25}=2\)

=>\(\sqrt{\left(x-5\right)^2}=2\)

=>\(\left|x-5\right|=2\)

=>\(\left[{}\begin{matrix}x-5=2\\x-5=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\\x=3\end{matrix}\right.\)

d: \(\sqrt{x^2-14x+49}-5=0\)

=>\(\sqrt{x^2-2\cdot x\cdot7+7^2}=5\)

=>\(\sqrt{\left(x-7\right)^2}=5\)

=>|x-7|=5

=>\(\left[{}\begin{matrix}x-7=5\\x-7=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=12\\x=2\end{matrix}\right.\)

\(a,\sqrt{4x-20}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9x-45}=4\left(đkxđ:x\ge5\right)\\ \Leftrightarrow\sqrt{4\left(x-5\right)}+\sqrt{x-5}-\dfrac{1}{3}\sqrt{9\left(x-5\right)}=4\\ \Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}-\sqrt{x-5}=4\\ \Leftrightarrow2\sqrt{x-5}=4\\ \Leftrightarrow\sqrt{x-5}=2\\ \Leftrightarrow x-5=4\\ \Leftrightarrow x=9\left(tm\right)\)

\(b,\sqrt{2x-1}-\sqrt{8x-4}+5=0\left(đkxđ:x\ge\dfrac{1}{2}\right)\\ \Leftrightarrow\sqrt{2x-1}-\sqrt{4\left(2x-1\right)}=-5\\ \Leftrightarrow\sqrt{2x-1}-2\sqrt{2x-1}=-5\\ \Leftrightarrow-\sqrt{2x-1}=-5\\ \Leftrightarrow\sqrt{2x-1}=5\\ \Leftrightarrow2x-1=25\\ \Leftrightarrow2x=26\\ \Leftrightarrow x=13\left(tm\right)\)

\(c,\sqrt{x^2-10x+25}=2\\ \Leftrightarrow\sqrt{\left(x-5\right)^2}=2\\ \Leftrightarrow\left|x-5\right|=2\\ \Leftrightarrow\left[{}\begin{matrix}x-5=2\\x-5=-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=7\\x=3\end{matrix}\right.\)

\(d,\sqrt{x^2-14x+49}-5=0\\ \Leftrightarrow\sqrt{\left(x-7\right)^2}=5\\ \Leftrightarrow\left|x-7\right|=5\\ \Leftrightarrow\left[{}\begin{matrix}x-7=5\\x-7=-5\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=12\\x=2\end{matrix}\right.\)

a: Ta có: \(\sqrt{4-3x}=8\)

\(\Leftrightarrow4-3x=64\)

\(\Leftrightarrow3x=-60\)

hay x=-20

b: ta có: \(\sqrt{4x-8}-12\sqrt{\dfrac{x-2}{9}}=-1\)

\(\Leftrightarrow2\sqrt{x-2}-12\cdot\dfrac{\sqrt{x-2}}{3}=-1\)

\(\Leftrightarrow x-2=\dfrac{1}{4}\)

hay \(x=\dfrac{9}{4}\)

\(\left\{{}\begin{matrix}8>0\left(luondung\right)\\4-3x=64\end{matrix}\right.\) \(\Leftrightarrow x=-20\left(ktm\right)\)

a) \(\sqrt{7+\sqrt{2x}=3+\sqrt{5}}\)   (x≥0) Đặt \(\sqrt{2x}\) = a ( a>0 )

Khi đó pt :

<=> 7+a =3 + \(\sqrt{5}\)

<=> 4+a = \(\sqrt{5}\)

<=> (4+a)\(^2\) = 5

<=> 16 + 8a + a\(^2\) = 5

<=>a\(^2\) + 8a+ 11 = 0

<=> a = -4 + \(\sqrt{5}\) (Loại) và a = -4-\(\sqrt{5}\)(Loại) 

Vậy Pt vô nghiệm.

b) \(\sqrt{3x^2-4x}\) = 2x-3

<=> 3x\(^2\)- 4x = 4x\(^2\)-12x + 9 

<=> x\(^2\)-8x+9 = 0

<=> x=1 , x=9 

Vậy S={1;9} 

c\(\dfrac{\left(7-x\right)\sqrt{7-x}+\left(x-5\right)\sqrt{x-5}}{\sqrt{7-x}+\sqrt{x-5}}\) = 2

<=> \(\dfrac{\left(\sqrt{7-x}\right)^3+\left(\sqrt{x-5}\right)^3}{\sqrt{7-x}+\sqrt{x-5}}=2\)

<=> \(\dfrac{\left(\sqrt{7-x}+\sqrt{x-5}\right)\left(7-x-\sqrt{\left(7-x\right)\left(x-5\right)}+x-5\right)}{\sqrt{7-x}+\sqrt{x-5}}=2\)

<=> \(\sqrt{\left(7-x\right)\left(x-5\right)}=0\)

<=> x=7,x=5

Vậy x=5 hoặc x=7