Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b).Ví dụ, trong Hình 1.12a, độ dốc của đồ thị li độ - thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t...
Đọc tiếp
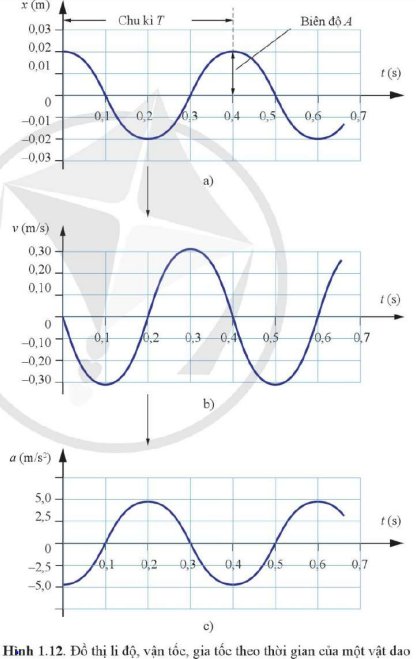
Dựa vào độ dốc của đồ thị li độ - thời gian, ta có thể xác định vận tốc của xe kĩ thuật số tại mỗi thời điểm. Từ các số liệu này có thể vẽ được đồ thị hình sin biểu diễn sự liên hệ giữa vận tốc và thời gian (Hình 1.12b).
Ví dụ, trong Hình 1.12a, độ dốc của đồ thị li độ - thời gian bằng 0, vận tốc bằng 0. Khi t tăng từ 0 s đến 0,2 s, độ dốc âm, vận tốc có giá trị âm. Tại t = 0,2 s, độ dốc bằng 0 một lần nữa. Từ t = 0,2 s đến t = 0,4 s, độ dốc dương, vận tốc có giá trị dương. Độ dốc của đồ thị li độ - thời gian có độ lớn cực đại tại các thời điểm t = 0,1 s; 0,3 s; 0,5 s; …
Bằng cách tương tự, dựa vào độ dốc của đồ thị vận tốc – thời gian ở Hình 1.12b, ta có thể tìm được gia tốc của xe tại mỗi thời điểm và vẽ được đồ thị hình sin như Hình 1.12c.
Dựa vào các đồ thị ở Hình 1.12, tìm:
Các thời điểm gia tốc của xe bằng 0.
Các thời điểm gia tốc của xe cực đại.
Giải thích cách làm.
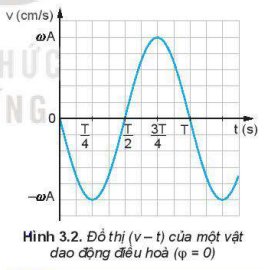
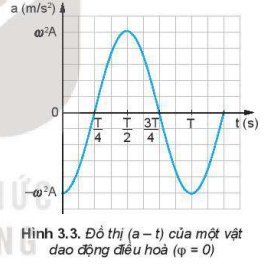

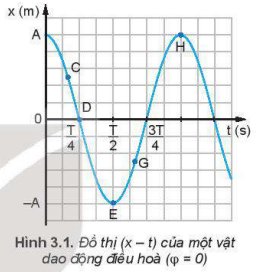



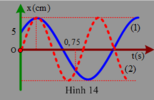
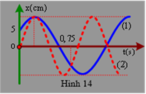
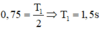
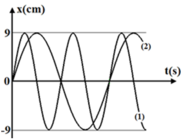
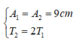
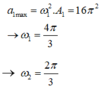
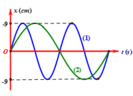


Trên đồ thị (v – t) Hình 3.2, tại thời điểm \(\dfrac{T}{4}\), \(\dfrac{3T}{4}\) độ dốc của đồ thị bằng 0 và tại thời điểm 0, \(\dfrac{T}{2}\), T độ dốc của đồ thị cực đại. Trên đồ thị (a - t) Hình 3.3 thì ngược lại.